
Читайте также:
|
Преимущества параметрической формы представления криволинейных объектов [24]:
- возможность локального контроля формы объекта;
- гладкость и непрерывность в математическом смысле;
- возможность аналитического вычисления производных;
- устойчивость к малым возмущениям.
Процесс формирования кривой желательно организовать так, чтобы каждый сегмент строился индивидуально, а не строить все сегменты единой глобальной вычислительной процедурой. Желательно свести процедуру к выбору небольшого ансамбля опорных точек, которые будут полностью характеризовать форму сегмента кривой. Через опорные контрольные точки сегмент проходит, а некоторые располагаются вблизи действительной кривой. В задачах компьютерной графики предпочтение отдается классу полиномиальных кривых, которые называются сплайнами. Название сплайны произошло от английского наименования деревянной рейки, с помощью которой в кораблестроении вычерчивались гладкие контуры.
5.6. Параметрическая непрерывность
На рисунке 5.2 показаны два последовательных сегмента составной параметрической кривой. Обозначим полином левого сегмента р(u), а полином правого - q(u). Сформулируем разные условия непрерывности, сопоставляя значения полиномов и их производных в точке сопряжения для u =1 для р(u) и u =0 для q(u). Если желательно, чтобы составная кривая была непрерывной необходимо в точке сопряжения обеспечить выполнение условия:
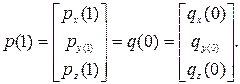

Рис. 5.2. Непрерывность составной кривой в точке сопряжения
В точке сопряжения значения всех трех параметрических компонентов векторов р и q должны быть равны. Кривые, в которых такие удовлетворяются, назовем кривыми, обладающими параметрической непрерывностью класса  .
.
Переходя к анализу производных в точке сопряжения, можно сформулировать условие непрерывности по первой производной:
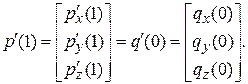
Кривые, в которых условия непрерывности удовлетворяются и для значения, и для первой производной, назовем кривыми, обладающими параметрической непрерывностью класса С 1.
Дата добавления: 2015-07-11; просмотров: 102 | Нарушение авторских прав