Читайте также:
|
Производная к кривой, заданной параметрически, в некоторой точке есть вектор касательной к этой кривой, направленный в сторону увеличения значения параметра. В точке сопряжения вместо равенства значений компонент производной к сегментам потребуем только соблюдения пропорциональности этих компонент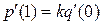 
с некоторым коэффициентом k.
Если касательные к обоим сегментам пропорциональны, то соответствующие векторы параллельны, но имеют разную длину. Считается, что составная кривая, удовлетворяющая этим условиям, обладает геометрической непрерывностью класса G 1.
Форма кривой, обладающей геометрической непрерывностью класса G 1, зависит от коэффициента пропорциональности длин касательных к сегментам в точке сопряжения. Форма сегментов кривых, совпадающих в конечных точках и имеющих в этих точках пропорциональные векторы касательных, довольно существенно отличается (рис. 5.3). Это свойство используется в графических программах, в которых пользователю предоставляется возможность регулировать значение коэффициента пропорциональности векторов касательных и таким способом настраивать желаемую форму вычерчиваемой кривой.
Рис. 5.3. Влияние длины векторов касательных на форму сегмента
полиномиальной кривой
Дата добавления: 2015-07-11; просмотров: 206 | Нарушение авторских прав