Представление кривых и поверхностей в явной форме

КРИВЫЕ И КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ

Обычно если в компьютерной графике возникает необходимость включить в состав сцены криволинейный объект, например сферу, то его зачастую стремятся с самого начала приближенно представить (аппроксимировать) множеством плоских многоугольников. Альтернативный способ состоит в том, чтобы предоставить пользователю средства работы с криволинейными объектами. Наиболее широкое распространение в компьютерной графике получили следующие виды подобных объектов: кривые и поверхности Безье, B-сплайны [1, 3, 11, 12, 15, 22, 24].

Представление кривых и поверхностей в явной форме

Явная форма представления кривой в двухмерном пространстве имеет вид уравнения, в левой части которого стоит зависимая переменная, а в правой части - функция, аргументом которой является независимая переменная. В пространстве переменных х, у уравнение линии в явной форме имеет вид:

Некоторые функции f имеют обратную g, которая позволяет изменить назначение зависимой и независимой переменных в уравнении, т.е. выразить x как функцию от у:

В трехмерном пространстве линия описывается системой из двух уравнений в явной форме, например, переменная х снова выбрана в качестве независимой, то имеем два уравнения зависимых переменных:

,

.

Для описания поверхности потребуется использовать две независимые переменные. Уравнение поверхности в явном виде будет выглядеть так:

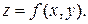
Дата добавления: 2015-07-11