
Читайте также:
|
В параметрической форме значение каждой координаты точки, принадлежащей кривой является функцией независимой переменной u, которая называется параметром кривой. В трехмерном пространстве кривая описывается системой из трех параметрических уравнений:

Одно из главных достоинств параметрической формы представления - ее единообразие в двух- и трехмерном пространствах. В первом случае нужно просто отбросить третье уравнение для координаты z.
Для описания поверхности в параметрической форме требуется использовать два параметра. Система уравнений поверхности имеет вид:
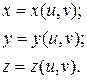
Изменяя значения параметров u и v в некотором интервале, можно сформировать значения координат всех точек поверхности.
Параметрическая форма описания кривых и поверхностей является, во-первых, наиболее гибкой, а во-вторых, устойчивой к любым вариациям формы и ориентации объекта, что делает ее особенно удобной для использования в математическом обеспечении компьютерной графики.
Дата добавления: 2015-07-11; просмотров: 102 | Нарушение авторских прав