Читайте также:
|
Пусть функция 
задана на множестве X за исключением б.м. точки 
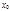. Возьмем на множестве X последовательность точек, отличных от . 
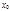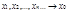(1). Значения функций в этих точках также образуют посл-ть: 
(2)
Опр.1: Число A называется пределом функции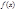 
в точке 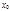если для любой посл-ти точек (1) из X, отличных от 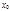и сходящихся к 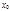, посл-ть соот-их значений функции (2) сх-ся к числу A. 
.
Опр.1.1: Число A называется пределом функции 
в точке 
, если для любого 
существует 
из нер-ва 
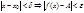
из 
Опр.2.: Функция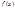 
называется непрерывной в точке 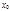,если выполняется тождество 
Рассмотрим последовательномть точек 
. Обозначается 
.
Пусть функция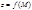 
определена на некотором множестве 
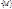и точка 
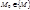или 
, но обладает тем свойством, что в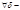 
окрестности этой точки содержится хотя бы одна точка множества 
, отличная от 
.
Опр.3.: ЧислоA называется пределом функции 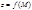в точке , если для любой последовательности точек 
соответствующая последовательность значений функции 
сх-ся к A.
Опр.4.: Функция 
называется непрерывной в точке , если предел функции в этой точке сущ-ет и равен значению функции в этой точке, т.е. 
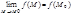или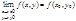 
.
Дата добавления: 2015-07-11; просмотров: 228 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Слабые аргументы | | | Свойства функций непрерывных на отрезке. |