Читайте также:
|
Пусть функция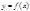 
определена в промежутке X. Исходя из некоторого значения 
независимой переменной, придадим ему приращение 
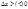, не выводящее его из промежутка X, так что и новое значение 
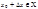. Тогда 
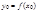заменится новым значением 
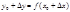, т.е. 
.
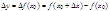Опр.: Если существует предел отношения приращения функции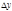 
к вызвавшему его приращению независимой переменной 
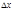, при стремлении 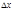к 0,т.е. 
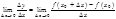, то он называется производной функции 
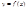по независимой переменной x при данном её значении (или в данной точке) .
Пусть имеем функцию 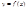, определённую на X и непр. в точке 
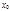. Тогда приращению 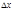аргумента отвечает приращение 
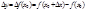, беск. малое вместе с 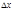. При А=0 наличие равенства 
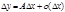(1) показывает, что беск. малая 
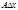(линейная относительно 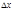беск. малая, 
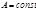) эквивалентна беск.малой 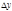и значит служит для последней её главной частью, если за основную беск.малую взять .
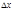Опр.: Дифференциалом функции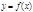 
в точке 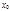называется главная линейная относительно 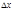часть приращения функции в этой точке: 
.
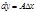Формула Лейбница для n-ой производной произведения 2-х функций: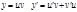 
… 
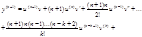
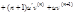
Для n-го дифференциала функции справедлива формула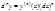 
.
Утверждение: Для того чтобы функция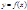 
в точке 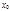была дифференцируема, Н. и Д., чтобы для неё в этой точке существовала конечная производная 
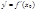. При выполнении этого условия равенство (1) имеет место при значении постоянной A, равной именно этой производной: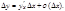 
Дата добавления: 2015-07-11; просмотров: 192 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства функций непрерывных на отрезке. | | | Функции нескольких переменных. |