Читайте также:
|
Если функция 
непрерывна на 
, то какая бы ни была её первообразная на , справедлива формула: 
Опр.: Функция 
называется первообразной для функции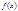 
на некотором промежутке, если для всех значений 
из этого промежутка выполняется равенство: 
.
Справедлива также следующая формула интегрирования по частям: 
Формула замены: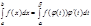 
Формула Эйлера: 
подстановка 
Дата добавления: 2015-07-11; просмотров: 245 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В.3. Определённый интеграл и его свойства. Основная формула интегрального исчисления. | | | В.4.Числовые ряды. Абсолютная и условная сходимость. Признаки сходимости: Даламбера, интегральный, Лейбница. |