Читайте также:
|
Используя вид полинома Лагранжа и свойства производных для полинома, можно построить оценку для погрешности интерполяционного полинома. Это не вычислительная, а неустранимая (та, которая зависит от полученных значений) погрешность, связанная с неточностью замены одной функции на другую. Вычислительная погрешность тоже существует и должна быть добавлена к неустранимой. Правда для малых порядков полиномов она гораздо меньше и может не учитываться для полиномов Лагранжа и Ньютона. Для оценки погрешности интерполяционного полинома получают формулу вида:
, где х* - некая точка на отрезке интерполяции,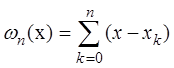 
функция-простой полином с равными 1 коэффициентами для оценки выберем максимальное значение формулы => 
Дата добавления: 2015-07-11; просмотров: 110 | Нарушение авторских прав