Свойства коэффициентов Котеса.

1) – нормировка

2) – симметричность.

– не зависят от пределов интегрирования.

Частные случаи формул:

1) Если порядок полинома n=0, то C₀ =1 => I= (b-a)*f(a) - формула левого прямоугольника или I= (b-a)*f(b) - формула правого прямоугольника.

2) Если n=1, то C₀ = C₁ = => I=(b-a)* - формула трапеции.

3) Если n=2, C₀ = C₂ = 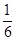, = => I= * + , где точка с=(b+a)/2. это формула парабол или Симпсона.

Название этих формул имеет геометрический смысл. Как известно, интеграл равен площади фигуры, ограниченной графиком функции и осью Х. Полином нулевого порядка – константа => его график прямая параллельная оси Х. Это значит, что в методе прямоугольников мы заменяем площадь фигуры прямоугольником. Его основание – отрезок интегрирования [a,b], а высота – значение функции f(x). Значение функции можно выбирать на левом конце отрезка f(a) или на правом f(b).

Для метода трапеций полином имеет 1-й порядок – это прямая, которая имеет наклон (f(a) + f(b)/2). Таким образом, мы заменяем площадь фигуры трапецией.

Для метода Симпсона полином имеет 2-й порядок – это парабола, которая должна проходить через 3 точки. Поэтому, мы вынуждены кроме точек a и b брать еще точку середины отрезка с=(a+b)/2.

Характерно, что формула трапеции может быть получена как среднее (полу сумма) формул левых и правых прямоугольников. Теперь эти формулы можно использовать для получения многократных методов.

– многократный метод левых прямоугольников h=

- многократный метод правых прямоугольников

- многократный метод трапеций.

Более сложно выглядит формула метода парабол. Здесь необходимо учитывать, что формула Симпсона требует не четного количества узлов (четного количества отрезков n), либо дополнительного включения промежуточных узлов. Таким образом, если число отрезков n- четно, то все узлы кроме крайних делятся на четные и нечетные:

Здесь суммирование ведется либо по узлам с четным, либо с нечетным номером.

Замечание. Следует учитывать, что для многократного метода погрешность является суммой погрешностей каждого отрезка. Поэтому, общая погрешность будет больше и даже уменьшится порядок точности.

Дата добавления: 2015-07-11