Понятие графа, методы описания графа, виды графов. Эйлеровы и гамильтоновы графы.

Пусть X - произвольное непустое множество и Х 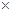Х - его декартов квадрат, т.е. множество всех упорядоченных пар (x₁, x₂)из элементов множества X. Если множество X - конечно и состоит из п элементов, то его декартов квадрат Х 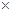Х содержит п² пар, и пары (x₁, x₂)и (x_2, , x₁) являются различными элементами множества Х 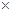Х при 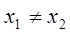- Иногда множество Х 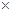Х называют упорядоченным произведением множества X на себя.

Рассмотрим теперь так называемое неупорядоченное произведение Х&Х множества X на себя, которое определяется как множество всех неупорядоченных пар из элементов множества X. Элементы из Х&Х будем обозначать (х₁&х₂). Ясно, что во множестве Х&Х пары (х_} &х₂) и (х₂ &x₂) не различимы. Если множество X - конечно и состоит из п элементов, то множество Х&Х содержит 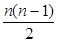элементов.

Графом G(V, E, f) называется совокупность непустого множества V, изолированного от него произвольного множества Е и отображения f:E—> V&V множества Е в V&V, которое каждому элементу из Е ставит в соответствие некоторый элемент из V&V. При этом множества V и Е называются соответственно множеством вершин и множеством ребер графа G(V, Е, f), а отображение f называется отображением инциденции этого графа.

часто вершины и ребра графа объединяются одним общим термином - элементы графа.

граф G это совокупность двух множеств: вершин V и ребер Е, между элементами которых определено отношение инцидентности - каждое ребро е 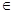Е инцидентно ровно двум вершинам v', v" 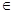V, которые оно соединяет. При этом вершина v' (v") и ребро е называются инцидентными друг другу, а вершины v' и v ", являющиеся для ребра е концевыми точками, называются смежными

Ребро, соединяющее две вершины, может иметь направление от одной вершины к другой; в этом случае оно называется направленным, или ориентированным, или дугой и изображается стрелкой, направленной от вершины, называемой началом, к вершине, именуемой концом.

Граф, содержащий направленные ребра (дуги) с началом v' и концом v", называется ориентированным (орграфом), а ненаправленные – неориентированным.

Ребра, инцидентные одной и той же паре вершин, называются параллельными, или кратными.

Граф, содержащий кратные ребра, именуется мулътиграфом. Ребро, концевые вершины которого совпадают, называется петлей.

Граф называется конечным, если множество его элементов (вершин и ребер) конечно.

Замечание. Мы будем рассматривать неориентированные графы без петель и кратных ребер.

Граф без петель и кратных ребер именуется полным, если каждая пара вершин соединена ребром. По-другому, граф называется полным, если каждая вершина соединена со всеми остальными.

Дополнением графа G называется граф G, имеющий те же вершины, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, чтобы получить полный граф.

Локальной степенью (или просто степенью) вершины v 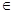V графа G называется количество ребер 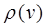, инцидентных вершине v.

Дата добавления: 2015-07-11