Читайте также:
|
В комбинаторном анализе изучаются различные объекты, порождаемые элементами из конечного множества А= {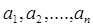 
}, и числовые характеристики этих объектов. Часто рассматриваются, например, упорядоченные или неупорядоченные подмножества множества А, подмножества с повторяющимися элементами из множества А и т. д. Вместе с классами таких комбинаторных объектов естественным образом вводятся и так называемые комбинаторные числа, задающие число объектов в том или ином классе и зависящие от некоторых параметров, например, от мощности исходного множества А и мощности рассматриваемых подмножеств множества А.
Размещения элементов. Пусть А = {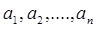 
}. Размещением элементов из А по k (или размещением из n элементов по k) называется упорядоченное подмножество из k элементов множества А.
Для А = {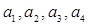 
} размещениями из А по 3 будут, например, { 
}, { 
}, { 
}.
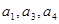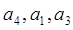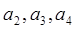Обозначим число размещений из n элементов по k через A(n, k). При построении конкретного размещения первым элементом в нём можно взять любой из n элементов множества А, вторым элементом — любой из n — 1 оставшихся в А элементов и т. д. Поэтому
A(n, k) = n(n- 1 )...(n-k+ 1 ) при 1 < k < n.
Или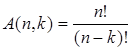 
При k > n не существует размещений из n по k, следовательно, A(n, k)= 0 при k >n; при k = 0 полагаем A(0,0) = A(n,0)= 1. Нетрудно заметить, что для чисел A(n, k) выполняются тождества
A(n, k) = n A(n-1, k-1)
A(n, k) = A(n, k-1)(n=k+1)
Перестановки элементов. Перестановками элементов множества А = { 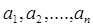} (или перестановками из n элементов) называются всевозможные упорядоченные множества из n элементов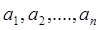 
Для A ={ a1,a2,a3 } перестановками будут: { a1,a3,a2 }, { a2,a1,a3 }, { a2,a3,a1 }.
Перестановки из n элементов — частный случай размещений из n элементов по n. Поэтому
P(n)=n!
Сочетания элементов. Сочетанием элементов из А = {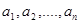 
} по k (или сочетанием из n элементов по k) называется неупорядоченное подмножество из k элементов множества А.
Для А — { a1,a2,a3 } всевозможными сочетаниями по 2 элемента будут { a1,a2 }, { a1,a3 }, { a2,a3 }.
В сочетании, в отличие от размещения, порядок следования элементов не учитывается. Поэтому из одного сочетания (из n элементов по k) получается k размещений. Отсюда для числа C(n,k) сочетаний из n элементов по k получается формула
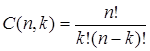
Сnk=Ank/k!
Cnk=(n*(n-1)*(n-2)*...*(n-k+1))/k!
Из формул видно, что:
Cn0=1,
Cn1=n,
Cn2=n*(n-1)/2=(n2-n)/2,
Cn3=n*(n-1)*(n-2)/6
...
Cnn-1=n,
Cnn=1.
Свойство 1. Cnk=Cnn-k (при всех n>=0 и всех k от 0 до n; обычно говорят кратко - "при всех n и k").
Доказательство: Их у этого свойства будет два: первое - из формулы, второе - комбинаторное рассуждение.
1.) Cnk=n!/(k!*(n-k)!), а Cnn-k=n!/((n-k)!*(n-(n-k))!)=n!/((n-k)!*k!) - то же самое, что и Cnk, ч.т.д.
2.) Когда мы выбираем k предметов из n, то n-k предметов мы оставляем. Если мы, наоборот, выбранные k предметов оставим, а оставленные n-k - выберем, то получим способ выбора n-k предметов из n. Заметим, что мы получили взаимно-однозначное соответствие способов выбора k и n-k предметов из n. Значит, тех и других способов поровну. Но одних а Cnk, а других а Cnn-k, поэтому они равны, ч.т.д.
Свойство2. Cn+1k+1=Cnk+Cnk+1, при всех n и k.
Доказательство:
1.) Cnk=n!/(k!*(n-k)!), Cnk+1=n!/((k+1)!*(n-k-1)!), а Cn+1k+1=
2.) (n+1)!/((k+1)!*(n-k)!). Теперь приведем первые два равенства к общему знаменателю и сложим: Cnk+Cnk+1 = n!*(k+1)/((k+1)!*(n-k)!)+n!*(n-k)/((k+1)!*(n-k)!) = n!*(k+1+n-k)/((k+1)!*(n-k)!) = (n+1)!/((k+1)!*(n-k)!) = Cn+1k+1, ч.т.д.
Размещением с повторением из n элементов по m или упорядоченной (n, m)- выборкой с возращениями называется любой кортеж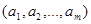 
элементов множества М, для которого 
.
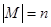Поскольку в кортеж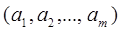 
на каждое место может претендовать любой из n элементов множества М, число размещений с повторениями 
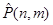равно 
:
.
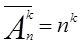Пример. Из цифр 1, 2, 3, 4 можно составить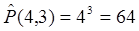 
трехзначных числа.
Определим отношение эквивалентности на множестве размещений с повторениями из n по m: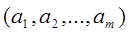 
~ 
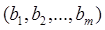
для любого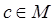 
число элементов 
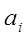, равных c, совпадает с числом элементов 
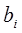, равных c.
Сочетания с повторениями элементов. Сочетанием с повторениями элементов из А= {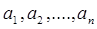 
} по k (или сочетанием с повторениями из n элементов по k) называется неупорядоченный набор из k элементов, в котором элементы могут повторяться и каждый элемент сочетания встречается в А.
Другими словами, сколькими способами можно разместить эти предметы в ящиках, если разрешается помещать сколько угодно предметов в ящик.
Формула для числа сочетаний с повторениями: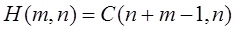 
Когда распределяем 2 предмета в один ящик, то можно сказать, что помещаем в два ящика по одному предмету.
Если мы добавим n-1 ящик, то любую комбинацию, при которой в ящиках по несколько предметов, можно представить в виде комбинации заполнения с помощью дополнительных ящиков по одному предмету. В результате необходимо величину m увеличить на n-1 и задача будет сведена к задаче без повторений.
Пример. Число различных бросаний двух одинаковых кубиков равно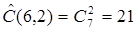 
.
Дата добавления: 2015-07-11; просмотров: 105 | Нарушение авторских прав