Разбиения

Разбиения не были рассмотрены среди типовых комбинаторных конфигураций, потому что получить для них явную формулу не так просто, как для остальных.

Пусть 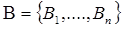есть разбиение множества Х из m элементов на n подмножеств:

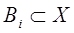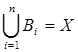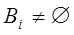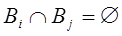, , , при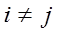

Подмножества 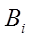называются блоками разбиения.

Между разбиениями и отношениями эквивалентности существует взаимнооднозначное отношение. Есл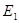и и 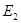- два разбиения Х, то говорят, что разбиение 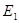есть измельчение разбиения 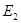, если каждый блок 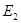есть объединение блоков .

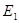Если k =2, упорядоченное разбиение множества М на два подмножества, имеющие соответственно 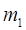и 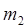элементов, определяется сочетанием (без повторений) из n элементов по 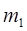или из n элементов по 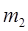(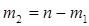). Следовательно, число разбиений R (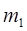, 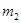) равно биноминальному коэффициенту 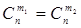. Таким образом,

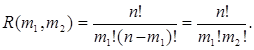
В общем случае число 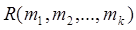упорядоченных разбиений (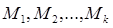), для которых 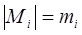, равно 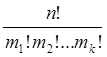, а число R(n, k) упорядоченных разбиений на k подмножеств вычисляется по формуле

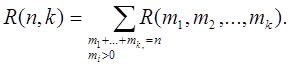
Числа 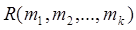называются полиномиальными коэффициентами, поскольку для всех 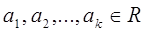справедливо соотношение

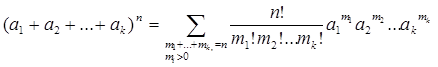
Пример. В студенческой группе, состоящей из 25 человек, при выборе старосты за выдвинутую кандидатуру проголосовали 12 человек, против – 10, воздержались – 3. Сколькими способами могло быть проведено такое голосование?

Пусть М – множество студентов в группе, 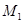- множество студентов, проголосовавших за выдвинутую кандидатуру, 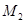- множество студентов, проголосовавших против, 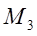- множество студентов, воздержавшихся от голосования. Тогда 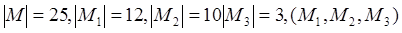- упорядоченное разбиение множества M. Искомое число R (12, 10, 3) равно .

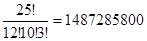Число 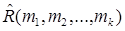разбиений исходного множества M на k подмножеств 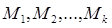, , 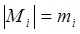неупорядоченных между собой, вычисляется по формуле

,

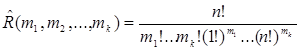а число всех возможных разбиений множества M на k подмножеств, неупорядоченных между собой, равно

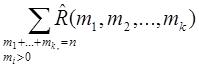
Пример. Сколькими способами из группы в 25 человек можно сформировать 5 коалиций по 5 человек?

Пусть X – множество людей в группе, 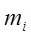- число коалиций по i человек, где i =1,…25. Тогда по условиям задачи 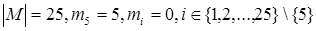, и, следовательно, искомое число будет равно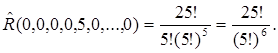

Теорема. Пусть S(n, k) – число разбиений множества n-X на k блоков. Тогда вычисление S(n, k) может быть выполнено рекурсивно на основе тождеств:

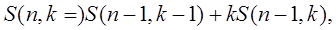
если 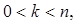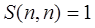, если n =0, 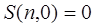, если n >0.

Доказательство. Для доказательства рассмотрим множество всех разбиений n-X на k подмножеств.

Это множество можно представить двумя пересекающимися классами: тех разбиений, которые содержат одноэлементный блок { n }, и тех, которые его не содержат. В этом случае n содержится по крайней мере в двухэлементном блоке. Мощность первого класса равна 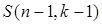, т. е. такова, каково число разбиений множества {1, 2, …, n -1} на k -1 блоков. Мощность второго класса равна 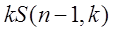, поскольку каждому разбиению множества {1, 2, …, n -1} на k -1 блоков соответствует в этом классе ровно k разбиений, образованных добавлением элемента n поочередно к каждому блоку. Доказательство окончено.

Числа S(n, k) называются числами Стирлинга второго рода. Рассчитанные по формулам (3.31)-(3.33), они могут быть представлены в виде треугольной таблицы – треугольника Стирлинга. Треугольник Стирлинга для значений n от 0 до 7 представлен в таблице.

Таблица

Дата добавления: 2015-07-11