Читайте также:
|
Классификация алгоритмических задач на графах
Задача сетевого планирования:
Пусть задана транспортная сеть с ориентированными дугами. У дуг заданы их длины. Требуется решить одну из следующих задач:
А) Найти длиннейший путь (без повторения) от входа к выходу вдоль направления стрелок. Путь считается больше, если сумма длин его дуг больше;
В) Определение длиннейшего или кратчайшего пути от входа к вершинам по направлению;
С) Определение тупиков и контуров в сети.
Тупик - висячая вершина, у которой есть входящий поток и нет выходящего.
Контур – простой цикл, построенный по направлению.
Задача поиска: алгоритмы поиска тупиков являются алгоритмами поиска всех вершин с определением степени входа и выхода для всех вершин Эти значения не могут быть = 0 
найдя нулевую степень мы найдем вершину, являющуюся тупиком.
Поиск контуров более сложная задача. Обычно решается удалением крайних вершин. Этот алгоритм убирает вершины и дуги, кот. не входят в цикл, а оставляя те, кот. входят. Как только мы не можем удалить ни одной дуги, то все оставшиеся являются циклическими. Тупики и контуры это ошибки при построении сетевого графика.
Задача о максимальном потоке
Сеть – связный граф, часть вершин которого выделена и наз-ся полюсами. Различают однополюсные и двухполюсные сети.
Транспортной сетью наз-ют двухполюсную сеть, в одном – исток, в другом – сток, они имеют направление и длину (пропускная способность сети).
Поток – это функция, которая определена на ребрах или дугах таким образом. Что она всегда положительна для любого ребра и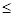 
его пропускной способности.
Для потоков должны выполняться законы Кирхгофа:
· в любой вершине сумма входящих потоков = сумме выходящих
· входной поток всей сети = выходному потоку данной сети
Сечением сети – наз-ся такое множество ребер, которые делят сеть на две части, со входом в одной стороне, с выходом – в другой. У каждого сечения можно просуммировать пропускную способность ребер. Эта величина наз-ся пропускной способностью сечения.
В задачах max и min пропускной способности сети требуется определить в соответствии с теоремой Форда-Фолкерсона, min пропускную способность простого сечения.
Простое сечение – сечение. У которого нет ребер, которые можно исключить.
Дата добавления: 2015-07-11; просмотров: 143 | Нарушение авторских прав