|
Читайте также: |
вх.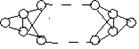 
вых
Max поток через сеть = min потоку через простое сечение.
Док-во: (методом моделирования).
Max поток через сеть существует и конечен, т.к. пропускная способность и кол-во дуг – конечные величины. Дуга наз-ся насыщенной, если max = пропускной способности.
Если бы все дуги были насыщены. То в сети был бы максимально возможный поток, но в реальности должны выполняться законы Кирхгофа, 
дуги не будут насыщены. Пусть в сети будет установлен максимальный поток. Проанализируем ситуацию, когда сеть разделена различными простыми сечениями. Т.к. простые сечения делят на две части, то входящий поток в сечение = max потоку. Расставим эти сечения по пропускной способности, в порядке убывания, , найдем сечение с min пропускной способностью. Докажем, что это сечение будет иметь только насыщенные ребра. Пусть одно ребро из min сечения не насыщенно, тогда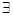 
возможность увеличить поток через данное сечение, сделав это ребро насыщенным. Т.о. min пропускная способность данного сечения позволит наращивать поток через него до тех пор, пока все ребра не будут насыщенными. Дальнейшее увеличение потока невозможно. Ч.Т.Д.
Дата добавления: 2015-07-11; просмотров: 173 | Нарушение авторских прав