Виртуальные машины Тьюринга. Нормальные алгорифмы Маркова.

Английский математик А. Тьюринг в 1937 г. опубликовал работу, в которой уточнял понятие алгоритма, прибегая к воображаемой вычислительной машине, известной теперь как машина Тьюринга. Основная идея машины Тьюринга и Поста заключалась в том, что алгоритмические процессы - это процедура, которые может совершать подходящее устройство «машина». На таких машинах оказалось возможным имитировать все алгоритмические процессы.

Абстрактным алфавитом (или просто алфавитом) конечное непустое множество символов, называемых буквами алфавита. Словами (или строками) в некотором алфавите А будем называть конечные последовательности букв этого алфавита. Длина слово-количество букв в нем. Слово нулевой длины называем пустым и обозначим «_» алфавит обозначим А, В, С….

Под машиной Тьюринга и Поста понимается некая гипотетическая (условная) машина, состоящая из следующих частей: 1. информационной ленты, представляемую собой бесконечную память машины. Лента разделена на ячейки, в котором можно записать один символ. Конечная совокупность символов алфавита, с которой работает машина, называется внутренним алфавитом. 2. «Головки чтения записи» - специального устройство, способного «считывать» символ ячейки. Головка представляется вдоль ленты вправо и влево так, что в каждый момент времени способна «видеть» только 1 ячейку. 3. Управляющее устройство, кот в каждый момент времени может находится в некотором состоянии, количество состояний, конечно. Состояние устройства управления называют внутреннимсостоянием машины. Одно из внутренних состояний называется заключительным состоянием. Переход к этому состоянию сигнализирует о конце работы. Совокупность состояний устройства управления называется внешним алфавитом. Цель работы МТ - в зависимости от слова, записанного на ленте(входное слово) переписать его так, чтобы на ленте было другое слово-результат.

Описание МТ. Пусть заданы внешний А={ 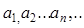} и внутренний алфавит P={ }. Лента бесконечна по обе стороны разбита на клетки. Запись символа в ячейку МТ приводит к замене ее содержимого. Головка чтения-записи может сдвигаться на одну вправо или влево или остаться неподвижной. Основной частью МТ является логический блок. Он имеет 2 входных канала: по одному из них поступает знак из ячейки, по другому знак того состояния, кот приписывается логическому блоку на данный такт. По выходному каналу логический блок посылает в текущую ячейку соот-щий знак 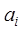, являющийся однознач-й функцией от сигналов (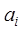, ) поданных на вход. Совокуп-ть, образован-я послед-тью состояний ячеек ленты и сост-ем лог-го блока, наз-ся конфигурацией или полным состоянием. Работает лог-й блок след-м образом:

1. Заставляет головку прочитать букву, кот-я стоит на ленте под ней.

2. В зависимости от прочит-й буквы и того состояния, в кот-м находится он сам,

а) заставляет головку записывать на ленте в той клетке, кот-я наход-ся под ней, некот-ю букву.

б) заставляет головку сдвинуться на одну ячейку вправо, влево или остаться на места

в) изменяет свое собственное положение.

3. Если в результате действий, в п.2, буква, располож-ная под головкой, положение головки и сост-ние лог. блока окажутся теми же, кот. были непосред-но перед выполнением этих действий, машина останавл-ся. В остал-ных случаях возвращается в п.1. Введем обозначения 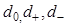для состоя-ия ленты(на месте влево вправо). Если головка читает букву и блок наход-ся в состоя-ии , тот поведение машины определяет запись означающую: «записать на ленте вместо букву 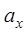, совершить перемещение ленты 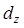, логическому блоку перейти в состояние ». Таким образом результатом может быть 3 ситуации: 1. Машина выполнила несколько шагов и остановилась, слово при этом не изменилось. 2. Машина выполнила несколько шагов, слово изменилось. 3. Машина никогда не остановиться, приводя к бесконечному изменению состояний. Остановка МТ осущест-ся в 3-х случаях: 1. внутрен-е состояние управляющего устройства не изменяется.

2. управляющее устройство остается на месте.

3. буква в противолеж-ей ячейке не изменяется.

Программа МТ. Совокупность команд, кот-е должна выполнить МТ для решения конкретной задачи наз-ся программой МТ. Начальной конфиг-ций сост-нии МТ, при кот-м на ленте занесена начальная информация обозначим . Будем считать МТ заданной если заданы ее внут-й и внеш-й алгоритмы. Представим работу МТ на примере.

Программа прибавления 1 к десятичному числу для машины Тьюринга

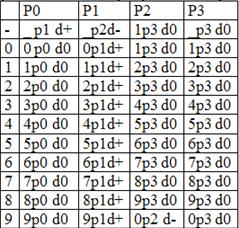
Пошаговое решение задачи

1. _18_-P0

2. _ 1 8_-P1

3. _1 8 _-P1

4. _18 _ -P1

5. _18_-P2

6. _19_-P3

7. _19_-P3- остановка

Остановка машины произойдет тогда, когда мы прибавим к числу 1, то есть вернемся к началу слова. Очев-о, что машина останавливается, если в состоянии P2 встречает цифры от 0 до 8 и когда встречает символ ‘_’, заменяя его при этом на 1.

Тезис Тьюринга. Любой конечный алгоритм м.б. реализован с помощью конечной программы МТ. Следов-но, если не сущест-ет прог-мы МТ для какой-либо задачи, то не сущ-ет и конечного алгоритма решения этой задачи. Соответ-вие, устанавливае-ое Маш Т между теми исходными данными, к которым она применима, и результатами ее работы, представляет некую функцию. Если для функции имеется машина, реализующая ее, то говорят, что вычислима по Тьюрингу. Функцию, для вычисления которой существует алгоритм, наз-т вычислимой. Любая вычислимая функция вычислима по Тьюрингу.

Машина Поста. Как и МТ относится к классу абстрактных машин, создана практически в тоже время, что и МТ. МП состоит из бесконечной ленты, вдоль, кот в обоих направ-ях перемещается каретка с головкой чтения-записи. Ячкйки ленты пронумерованы след-м образом (-3,-2,-1,0,1,2,3,)

-2 -1 0 1 2 В каждой ячейке ленты м.б. записан пустой символ «_» или символ-метка «» На каждом шаге каретка перемещается только в одну сторону. Состояние МП определяется сост-ем ленты(комбинация пустых и занятых ячеек) и номером ячейки, на кот настроена каретка. Работа МП состоит в том, что каретка передвигается вдоль ленты и записывает или стирает метки. Назовем командой одну зи 6-ти функций: 1. движение вправо. 2. движение влево. 3. запись. метки 4. 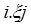стирание метки 5. передача управления. 6. 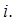стоп –остановка все числа натуральные. Пример. 137.= движ вправо 25.?(35,21) передача управления, 6386.стоп остановка.

Программа МП –конечный непустой список команд МП, обладающий след-ми св-ми: 1. Все команды послед-но пронумеров-ны, начиная с 1. 2. отсылка любой из команд (за исключением ком-ды стоп) есть номер одной команды прог-мы (включая номер той же команды).

Функционирование МП. Работа МП опред-ся согласно некот-й прог-ме и нача-му состо-ю. Будем считать, что в нач-м сос-нии каретка всегда настроена на ячейку с номером 0, т.е нач-ое сос-ие опред-ся только содержимым ленты. Уточним команды 1. сдвиг каретки вправо на 1-у ячейку и переход на команду с номером 1. 2. сдвиг каретки влево на 1-у ячейку и переход на команду с номером 3. записать метки в текущ-ю ячейку и переход на команду с номером 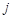(если в ячейке метка уже была, то команда не выполнима). 4. стирание метки в текущей ячейке и переход на команду с номером (если ячейка уже пуста, то команда не выполнима). 5. 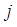если обозреваемая ячейка пуста, переход к команде с номером в противном случае к ₂. 6. МП останавливается. Выполнение команды может привести к 1-му из 3-х случаев: 1. Нормальная остановка по команде остановка. 2. аварийная ост-ка по невыполнимой команде. 3. зацикливание (бесконеч-я работа).

Тезис Поста. « числовая функция вычислима по Посту».

Дата добавления: 2015-07-11