Читайте также:
|
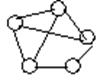
Оба алгоритма дают одно и то же дерево, которое имеет min длину.
Док-во.
1. Алгоритмы Прима-Краскала удаляют только циклические ребра или добавляют антициклические 
в результате должно получится дерево, соединяющее все вершины графа, т.е. остовное дерево.
2. Докажем, что алгоритмы П-К дают одинаковое дерево. Используем метод от противного.
Пусть Краскал дал дерево Гк, а Прим – Гп., кот. не равны. Сравним эти деревья и возьмем произвольную вершину А. По алгоритму Прима она соединена с остальными вершинами только одним ребром, кот. имеет min длину. А- последняя вершина алгоритма Прима. Найдем эту вершину в дереве Краскала. Если эта вершина соединена с остальными вершинами другим ребром, то образуется цикл, в кот. по алгоритму Краскала, мы должны удалить длиннейшее ребро получено противоречие. Поскольку удалено не длиннейшее ребро предположение о неравенстве деревьев ошибочно. Деревья одинаковы.
Дата добавления: 2015-07-11; просмотров: 237 | Нарушение авторских прав