Теорема Дейкстры

Алгоритм Дейкстры корректен, дает правильный результат для любого графа.

В качестве док-ва можно рассмотреть простые соображения – методом от противного.

Если бы из А в X существовал более короткий путь, то он обязательно отражался бы в одной из строчек столбца X₀, т.к. путь в X рассматривается из всех вершин. Т.о., наличие непроверенного короткого пути в X требует наличие таких же непроверенных путей для всех вершин этого пути, что в принципе невозможно Ч.Т.Д.

Существует удобный алгоритм Флойда-Уоршела Для решения задачи Дейкстры.

, где 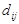- матрица кратчайших путей между вершинам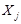и и .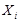

Вычисление по этой формуле в цикле по i, по j и внутри цикла k.

Этот алгоритм является следствием алгоритма Дейкстры, но находит расстояние между всеми вершинами. В результате он гораздо менее эффективен с точки зрения затраты времени на выполнение.

Дата добавления: 2015-07-11