Приведение задачи линейного программирования к стандартной форме

Любая задача линейного программирования может быть приведена к стандартной форме с помощью следующих преобразований:

1. Сделаем все неизвестные параметры неотрицательными. x_i ≥ 0

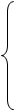x_k > a => x_k = x_k^’+a+ x_k^’’

x_k ≥ a => x_k= x_k^’+a

x_k < a => x_k = a- x_k^’- x_k^’’

x_k ≤ a => x_k = a- x_k^’

x_k- любое => x_k = x_k^’- x_k^’’

Если x_k- любое, то мы можем его представить как x_k = x_k^’- x_k^’’ при x_k ≥ 0, x_k^’’ ≥ 0. Таким образом, количество переменных увеличивается на одну. Принято новые переменные, которые нам потребуется ввести дополнительно называть избыточными.

x_k^’= x_k – a ≥ 0,

x_k^’= а - x_k ≥ 0, x_k ≤ a, следовательно, - x_k ≥ - a

x_k – a > 0

В этих случаях вводить новую переменную не надо.

x_k – a - x_k ≥ 0

x_k^’= x_k - а - x_k ≥ 0

x_k ≥ 0

если x_k < a, а - x_k>0

x_k^’= a - x_k - x_k ≥ 0

x_k ≥ 0

Если заменить эти неизвестные (и в целевой функции), то новые переменные со штрихом будут положительными.

2. Преобразуем неравенства в равенства:

∑ а^”_ij x_j≤ b^”_i (a)

∑ а^”_ij x_j ≥ b^”_i (б)

В случае (а) к сумме нужно прибавить избыточную переменную:

∑ а^”_ij x_j+х_изб= b”_i.

В результате описанных преобразований, ограничения в виде неравенств превратятся в ограничения в виде равенств. Если все ограничения преобразовать в равенства, то все элементы, стоящие справа в этой системе уравнений образуют вектор запаса b_i..

3. Когда вектор запаса получен, надо сделать его элементы неотрицательными b’_i≥ 0. Пусть в каком-то k -ом ограничении получено отрицательное значение:

∑ а’_kj x_j = b’_k<0

Здесь обозначено - ’’ (двойной штрих) - неравенство (матрица неравенств), ’ (один штрих) - для ограничений в виде равенств. Далее, в стандартной форме штрихами не будем пользоваться.

Существует два варианта нужного преобразования:

· Умножить все на -1

a_kj=- а’_kj

∑ а_kj x_j =- b’_k= b_k >0.

· Прибавить избыточную переменную

∑ а’_kj x_j+х_изб= b_k=0_.

При этом, любой из этих двух вариантов преобразования делает элементы вектора запаса неотрицательными.

О. Решение задачи ЛП – набор значений (вектор) переменных задачи ЛП.

О. Допустимое решение ЛП – решение задачи ЛП, которое удовлетворяет всем ограничениям задачи.

О. Область допустимых решений (допустимая область) – множество всех допустимых решений задачи ЛП.

О. Оптимальное допустимое решение – допустимое решение, для которого целевая функция имеет максимальное\минимальное значение целевой функции в допустимой области.

Ограничения в линейной задаче представляют в общем случае некие гиперплоскости. Для 2-х переменных это прямая, для 3-х переменных - плоскость, для 4-х и более переменных - гиперплоскость. При этом допустимая область для 2-х переменных – часть плоскости (многоугольник), для 3-х переменных – 3-х мерный многогранник, для 4-х и более переменных – многомерный многогранник. Характерной особенностью всех этих видов допустимых областей – наличие вершин, где пересекаются гиперплоскости.

Дата добавления: 2015-07-11