|
Читайте также: |
В общем случае задача численного интегрирования сводится к нахождению интеграла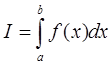 
с помощью приближенных формул. Численные методы при решении задачи интегрирования используются в следующих случаях:
а) Функция задаётся в виде таблицы значений или её значение вычисляется, как решение другой задачи (функция задаётся неявным видом).
б) Функция задана явно, но первообразную не возможно записать в явном виде.
Методы, используемые для решения задачи численного интегрирования можно разделить на однократные и многократные.
Однократный метод реализуется путем замены интегрируемой функции на ее аппроксимацию, которая имеет явную первообразную. Это дает возможность указать явную формулу для вычисления определенного интеграла.
Многократный метод - используем однократный метод, но весь отрезок интегрирования от а до b делим на n частей с шагом h=(b-a)/n c помощью точек 
.
На каждом участке [ xi-1, xi ] интеграл вычисляется однократным методом, а затем используя свойство аддитивности интегралов общий интеграл вычисляется как сумма интегралов на отдельных участках:
= 
.
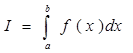Таким образом, основа формулы многократного метода – формула метода однократного. Смысл использования многократного метода – увеличение точности вычисления. Как правило формулы однократных методов таковы, что их погрешность быстро уменьшается при уменьшении отрезка интегрирования.
Одним из основных вариантов получения формул однократного метода является метод интегрирования интерполяционных полиномов. Если использовать полином Лагранжа, то получаются формулы, которые принято называть формуламиНьютона-Котеса:
- формула Ньютона – Котеса.
- коэффициенты Котеса. Для получения этого выражения для коэффициентов необходимо подставить в интеграл формулу полинома Лагранжа для равноотстоящих узлов. Затем делается замена переменных x’= n*(x-a)/(b-a) => и находим выражения, которые необходимо подставить в интеграл (xi–xj)=(b-a)*(i - j)/n,(x–xj)=(b-a)*(x’ - j)/n, dx’ = n*dx/(b-a).
Дата добавления: 2015-07-11; просмотров: 231 | Нарушение авторских прав