|
Читайте также: |
Подстановка (или замена переменной) базируется на следующей теореме.
Теорема 1. Если не удается найти интеграл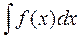 
непосредственно, то можно выбрать такую функцию x = j (t), удовлетворяющую условиям:
1) j (t) непрерывна при t Î (a; b), соответствующем интервалу x Î (a; b),
2) дифференцируемая при t Î (a; b);
3) имеет обратную функцию t = j -1(x), чтобы
| 
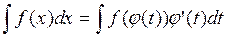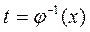
Был табличный или проще. Иногда для упрощения интеграла можно сделать замену t = y (x).
Замечание. Выбор правильной подстановки в значительной степени зависит от искусства вычислителя.
Дата добавления: 2015-07-10; просмотров: 107 | Нарушение авторских прав