Читайте также:
|
Ответ: 
Итак, любая рациональная дробь интегрируема. Для этого необходимо выполнить следующие действия.
1) Если дробь является неправильной, выделить ее целую часть. То есть представить в виде:
,
где Tm-n (x) и Rr (x) – многочлены степени m-n и r соответственно (причем r<n).
2) Разложить правильную рациональную дробь 
на сумму простых дробей
3) Вычислить интегралы от многочлена Tm-n (x) и каждой из простых дробей, полученных на шаге 2).
Пример 24.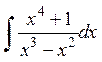 
1) Дробь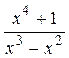 
- неправильная рациональная дробь. Выделим ее целую часть:
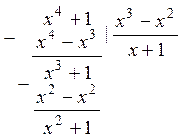
Поэтому можно записать:
2) Полученную правильную дробь 
разложим на сумму простых дробей:
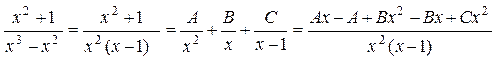
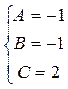
Отсюда следует: 
Значит, подынтегральная рациональная дробь представима в виде:
3) Найдем интеграл:
Ответ: 
Дата добавления: 2015-07-10; просмотров: 126 | Нарушение авторских прав