Читайте также:
|
Теорема 4. Пусть функция f (x) непрерывна на [ a;b ] и F (x) – какая-либо ее первообразная на [ a;b ]. Тогда определенный интеграл от функции f (x) по отрезку [ a;b ] равен разности значений функции F(x) в точках b и a: 
Доказательство. Из теоремы 3 следует, что наряду с функцией F(x) функция 
также является на [ a;b ] первообразной для f (x). Тогда по свойству первообразных для одной и той же функции на некоторой области имеем:
для любого x Î [ a;b ] (**)
Вычислим значение const. Для этого, используя свойство 1 определенного интеграла 
, рассмотрим равенство (**) при x = a:
Следовательно, равенство (**) можно переписать в виде:
для xÎ [ a;b ]
Теперь рассмотрим полученное равенство при x = b:
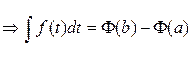
Это и есть формула Ньютона-Лейбница. Она является основной формулой интегрального исчисления, устанавливающей связь между определенным и неопределенным интегралами и дает правило вычисления определенного интеграла.
Замечание. Формулу Ньютона-Лейбница часто записывают в виде:
,
Где используется обозначение:
.
Дата добавления: 2015-07-10; просмотров: 220 | Нарушение авторских прав