|
Читайте также: |
Пусть функция f (x) определена и непрерывна на промежутке [ a;+¥) или (-¥; a ] или (-¥;+¥).
Определение 1. Если существует конечный предел 
, то этот предел называется несобственным интегралом от f (x) на бесконечном промежутке [ a;+¥), обозначается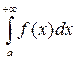 
и в этом случае говорят, что интеграл сходится. Если 
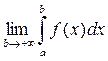не существует или равен ¥, то говорят, что интеграл 
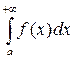расходятся.
Аналогично определяются интегралы:
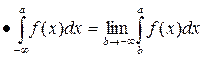
Если пределы конечные, то соответствующий интеграл считают сходящимся, а если хотя бы один из пределов не существует или бесконечный, то интеграл считают расходящимся.
Пример 1. Исследовать на сходимость несобственный интеграл:
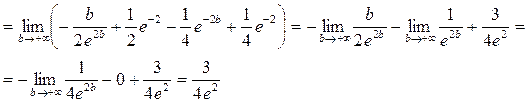
Так как получили конечное число, то интеграл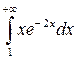 
сходится и равен 
.
Ответ: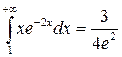 
Дата добавления: 2015-07-10; просмотров: 91 | Нарушение авторских прав