Читайте также:
|
ЧМ решения СЛУ
СЛУ запис-ся след образом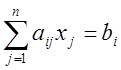 
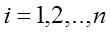. Коэф-ты 
образуют матрицу А сис-мы. Неиз-ные 
–вектор столбец неизвестных, В-вектор столбец правой части. В матричн. Форме СЛУ запис-ся след образом АХ=В. Иногда испол понят расширен матрицы сист, котор образ-ся путем присоед-я вектора столбца справа и обозн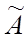 
.Эл-ты 
образ-ют главн диаг-ль матр, другие диаг-ли побочные. Для того, чтобы СУ имела 1 един реш-е необх, чтобы число урав было равно числу неизвестн; опред-ль матр А не равен 0.
L-матрицей наз матр, ниже главн диаг которой располож только 0. U-матр наз матр, выше главн диаг-ли которой располож только 0. L u U матр наз треугольными матр. Для численного реш-я СЛУ исп 2 типа методов - конечн и итерацион.
Конечн имеют строго определ кол-во операций.К ним относятся: М-д Гаусса, М-д полного исключения Жордано, Метод Халецкого. Кол-во операц в итерац методе завис от сх-ти этого метода.
Метод Гаусса
М-д Гаусса дел-ся на 2 этапа: прям и обратн ход. Прямой ход – с помощ эквивал-х преобраз-ний, не изменяющих реш-е сист, производ-ся исключение эл-тов, лежащих выше или ниже главн диаг. Сущ 2 вар-та:1. приведение матр к L(ниже гл.диог.0) или U(наоборот) виду; 2.в общем случае получить треуг матр.
Обратн ход исп для опред-я неиз-х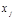 
. В кач-ве эквив преобраз, не изменяющих реш-е сист явл следующее преоб-ние матр 
:
1.делен или умнож строки на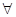 
постоян число, большее 0
2.слож или вычит 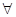2 строк
3.постр-е лин-х комбинац строк
4.перест-ка строк
5. переест-ка столб-в с одноврем измен-м индексов перем-х
Рассм процесс исключ прямого хода на примере получ-ия L-матр. Нужно исключ эл-ты, лежащ ниже главн диаг, при этом исключ-ем будет обращ-е в 0 этих эл-тов.Исключ-е произ-ся по столбцам, при этои базовым явл элемент главн диаг.
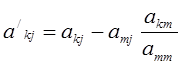
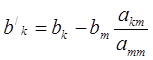
m=1,2,..,n-1
k=m+1,m+2,..,n
j=m,m+1,..,n
А для U-матр выпол
m=n,n-1…2
k=m-1,m-2,..,1
j=n,n-1,…,1
Точность выч-я по Гауссу опред-ся процессами округления в дан форме. Если диаг эл-т равен 0, то выч-ть нельзя, а если очень мал, то рез-т будет очень неточным. Сущ модификация м-да Гаусса за счет исп-я выбора главн эл-та. Главн эл-т – диаг эл-т, котор испол при вычисл.В процессе вычисл исп-ся все эл-ты главн диаг в кач-ве главн эл-тов, поэтому на главн диаг матр сист-мы желательно иметь макс по модулю эл-ты в своих столбцах или строках. Выбор такого эл-та может произ-ся либо перест-кой строк расшир матр, либо перест-кой столбцов. Во 2 случ необх переименовывать перем-ные. Чаще всего использ-ся 1 вар-т – переест-ка строк.
Т.о м-д Гаусса сущ 2 видов: просто м-д Гаусса и м-д Гаусса с выбором главн эл-та.
Расс обрат ход м-да Гаусса.Для L-матр:
k=n,n-1,n-2,..,1. Для U-матр:
k=1,2,.,n
М-д полного исключения Жордано
Жордан предложил исключ эл-ты не только выше, но и ниже главн диаг. В рез-те матр станов-ся полностью диаг-ной, т.е. все эл-ты кроме диаг-х равны 0.Для этого исключ можно восп той же формой. Но циклы в м-де Жордано по иному m=1,2,..,n-1; k 
m; j=1,..,n. Обратн ход в м-де Жордано прост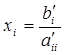 
, i=1,2,..,n
Штрих обозн, что это эл-ты расшир матр, преобразованные после процедуры исключения
Замеч1.В принципе в м-де Жордано можно исп выбор главн эл-та, но при этом сама процедура выбора очень сильно услож-ся, т.к. необх брать эл-ты как выше, так и ниже главн диаг. 2. В м-де Гаусса 2 этапа-прямой и обратн ход. Прямой ход обычно требует больше операций, чем обратный. М-д Жордано не имеет прак-ки обрат хода, а сост из 2 прямых ходов. Далее рассм м-д Халецкого.В нем нет прямого хода, а 2 обратн, но при этом произ-ся предварит преобр-е исходн матр.
Метод Халецкого
М-д сост в разлож-и матр сист в произвед матр U и L, при этом эл-ты главн диаг lii= 1. Сущ теорема алгебры, котор гласит, что для разлож произв матр А в произвед LU матриц необ и дост, чтобы все основн миноры были не равны 0. Для вырожд матр это условие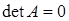 
. Для невырожд матр например 
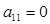, но любую невырожд матр можно путем перест-ки строк и столбцов привести к виду, в котором условие Сильвестра вып-ся, т.о перед разлож матр на LU нужно проверить ее на выпол-е условий сильвестра и при необ-ти произвести преобразование. Найдем формулы для опред-я эл-тов матр U и L. Выч-я будем производить последовательно по столбцам матр U и строкам матр L.
-столбцы матр U.
-строки матр L.
Особ-ть выч-я по найденным формулам сост в том, что необх выч-ть послойно. Сначала столбец U, потом строку L. Нужно учит, что в формуле для U - i 
j, а для матр L- j i.
Алгоритм м-да Халецкого следующий:
1. проверяем условие для матр сист её разложимости в произвед LU
2. послойно находим эл-ты матр L и U
3.проводим обратный ход для выч-я yi
4. проводим обратный ход для выч-я xi
Потенциально м-д Халецкого имеет наим кол-во операций по сравнению с м-дом Гаусса иЖордано, но реализац-я дан м-да имеет более сложн алг-мы. В то же время дан м-д может сильно экономить ресурсы компьютера,т.к. после получ матр UL, их можно хранить вместе в одной матр.
Сравнивая эти м-ды можно сделать вывод:
1.м-д Гаусса наибол. экономн вар-т, если сист рещ-ся 1 раз.
2.м-д Жордано удобен,если матр сист имеет много 0, а также в случ одноврем-го реш-я большого кол-ва уравн с 1 матр и разными столбцами правой части.
3.м-д Халецкого также наиб удобен при реш-и большого кол-ва уравн с одной матр сист.
ЧМ решения СЛУ
СЛУ запис-ся след образом 
. Коэф-ты 
образуют матрицу А сис-мы. Неиз-ные 
–вектор
-столбец правой части В. В матричн. Форме СЛУ запис-ся след образом АХ=В. Иногда испол понят расширен матрицы сист, котор образ-ся путем присоед-я вектора столбца справа и обозн 
.Эл-ты 
образ-ют главн диаг-ль матр, другие диаг-ли побочные. Для того, чтобы СУ имела 1 един реш-е необх, чтобы число урав было равно числу неизвестн; опред-ль матр А не равен 0.
L-матрицей наз матр, ниже главн диаг которой располож только 0. U-матр наз матр, выше главн диаг-ли которой располож только 0. L u U матр наз треугольными матр. Для численного реш-я СЛУ исп 2 типа методов - конечн и итерацион. Конечн имеют строго определ кол-во операций. Кол-во операц в итерац методе завис от сх-ти этого метода.
Итерационные м-ды реш-я СЛАУ.
При наличии сист уравн мы можем оперировать с понят-ми матр и вектора. Реш-е–это вектор в некот n-мер- ном лин прост-ве. В алгебре для векторов вводят числовую хар-ку-норму. В некот случ она имеет аналогию с длиной и расст. Норма должна удовл:
1.||αx||=||α|| ||x||
2.||x+y|| 
||x||+||y||
3.||x||=0 
x=0
Обычно определяют 3 разных нормы:
1.||x||1= 
-первая норма
2. 
-бесконечная норма
3. 
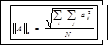-евклидова норма
Нормы векторов и матр д.б. согласованы с помощью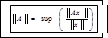 
Итерац м-ды осн-ны на итерац-х послед-х прибл-х, т.е. есть некая ф-ция, позвол наход k-ое прибл-е через (k-1) прибл-е
. х(0), х(1), х(2),.. сх-ся к вектору х, если 
Т.к. оценить сх-ть такой посл-ти невоз-но, то польз-ся косвенной оценкой погрешности, по которой 
- условие выхода или прекращ итерации.
Метод простой итерации
Пусть задана СУ АХ=В, котор запис-ся 
. Выразим в этой сист в кажд урав-нии по 1 перем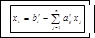 
, где 
;
-это матр, на диаг которой распол 0. У нас получилось Х=В’-A’X,
X(k)=B’-A’X(k-1)
В кач-ве нулевого прибл-я выбирают В’, т.е. Х(0)=В’. Сх-ть дан м-да, т.е. сущ-е предела посл-ти векторов док-ся теоремой.
Т: если матр сист А не вырожд и норма ||A’||<1, то дан м-д простой итерации будет сх-ся.
Замеч: т.о. сх-ть м-да прост итер-ии не завис от выбора нач приближ Х(0), а зависит только от матр сист. Усл-ем сх-ти будет след формула ||A’||<1.В кач-ве нормы м.б. выбрана любая из 3 норм. По 1 норме норма матр равна сумме модулей эл-тов столбца, котор имеет макс сумму. По бескон норме норма равна сумме модулей эл-тов строки, среди которых выбир-ся макс. Т.о. получ. Что либо 
Для всех строк
-условие диагон-го преобладания. Модуль эл-та главн диаг больше суммы модулей остальн эл-тов строки. Такое усл-е спр-во для всех строк.
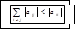
В дан случ диаг эл-т д.б. больше по модулю суммы модулей остальных эл-тов столбца. Это св-во спр-во для всех столбцов. Если же норма =1, то сказать о сх-ти ничего нельзя. Алгоритм простой итерац:
1.выбир Х(0)=В’ и преобраз матр сист к итерац виду
2.используем итер фор-лу и наход следующ приближ
3.сраним по фор-ле
норму с задан погр-ю. Если усл-е выпол, то прекращ выч-е, в противн случ возвр-ся к пункту2.
Метод Зейделя
Зейдель предложил усов-ть итерац ф-лу путем исп-я уже получ-х элем-тов вектора Х, тогда
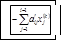. Каждое приближение сх-ся быстрее, чем у простой итерац, поэтому весь м-д сх-ся гораздо быстрее, кроме того в случае, когда м-д прост итерац не сх-ся, м-д Зейделя иногда сх-ся.
Метод координатной релаксации
Этот м-д заключ в следующем: после уточнения каждой коорд-ты по м-ду Зейделя, произв-ся смещение в том же направлении(смещение компонентов в одном и том же направл), на релаксационную часть этого смещения. Т.о. приближения отыскив-ся из соотнош
D-диагон матр с эл-ми 
по диаг-ли
При A>0 целесообразно брать показ-ль релаксации -1<p<1, в случае 0<p<1 м-д релаксации обычно наз м-дом сверхрелаксации. В частности, во многих случаях оптим-ной знач парам-ра релак-ции р опред-ся экспериментально. Иногда р зависит от n и i. Заключаем, что при
-1<p<1 всегда
, где F0(xn)- ф-ция, равная
F(x)+(AX,X)==(A(x-X),x-X)
Метод минимальных невязок
Для решения линейных систем уравнений можно применять и различные методы поиска экстремумов. Проблема решения системы уравнений заменяется эквивалентной задачей нахождения экстремума функции n переменных.
Одним из примеров является метод минимальных невязок. Вектор невязок определяется следующим образом.
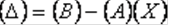
Очевидно, что если на место вектора (Х) подставить вектор решения, то второе слагаемое окажется равным вектору свободных членов и вектор невязок становится нулевым.
Таким образом, минимизация компонентов вектора невязок эквивалентна задаче решения уравнений. Что бы знак невязок не влиял на результат, минимизируют сумму квадратов невязок (скалярное произведение вектора на себя):
Запишем итерационную формулу поиска решения в следующем виде
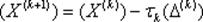
где индекс k обозначает номер итерационного шага, тау – константа, которую нам необходимо определить, Δ(k) (дельта) – вектор невязок на этом шаге.
Рассмотрим разность векторов невязок на двух последовательных шагах k и k+1
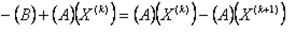
после подстановки имеем
Скалярное произведение этого вектора на себя имеет вид
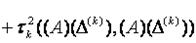
Параметр тау можно выбрать таким образом, чтобы левая часть была минимальной. Условием экстремума является равенство нулю производной по тау правой части выражения
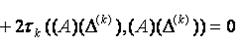
откуда,
Окончательно, k-ый шаг метода выглядит следующим образом:
1. Задается начальное приближение (Х(k))
2. Рассчитывается вектор невязок
3. Рассчитывается параметр тау. Для этого перемножается матрица коэффициентов и вектор невязок. Затем вычисляется его скалярный квадрат и произведение на матрицу невязок.
4. Рассчитывается новое приближение к вектору-решению
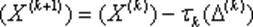
5. Проверяется один из критериев сходимости и, при необходимости, происходит переход к пункту 2.
6.
Дата добавления: 2015-07-11; просмотров: 125 | Нарушение авторских прав