Прямая и обратная задача теории погрешности.

Основной проблемой теории погрешности является поиск оценок. Выделяют прямую и обратную задачи теории погрешности.

1. Прямая задача: заданы приближённые величины А, B, C, D… и их абсолютные погрешности и функция . Требуется построить оценку погрешности функции . Для решения прямой задачи используется определение или метод разложения в ряд. Рассмотрим вариант определения.

А) Пусть дано , , ; требуется найти .

.

=

С помощью определений абсолютной и относительной погрешности можно построить таблицу погрешностей при математических вычислениях.

Абсолютная погрешность суммы равна сумме погрешностей.

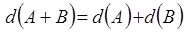
Для произведения : =

Для разности:

Следовательно, если производить вычитание близких величин, относительная погрешность может значительно возрастать.

Формула для оценки погрешности отношения :

Б) Оценивание погрешности разложением в ряд Тейлора.

Так как данная оценка бесконечна, то пользуются последовательными приближениями. В первом приближении 1 –й элемент ряда:

во втором соответственно второй - в третьем – d(A)=dF₂+ .

Формула для n - го приближения:

Очевидно, что нужно вычислять приближения последовательно, сначала вычислив 1-ое, проверить достаточно ли точна погрешность, затем второе и т.д.

Для функций двух аргументов F(A,B) разложение будет гораздо, сложнее:

dF≤(/sF/sA/)*d(A)+(/sF/sB/)*d(B)+(/s²F/sAsB/)*d²(A)+(/s²F/sB²/)*d²(B), где s – частная производная

На практике (для таких функций) ограничиваются первым приближением.

Обратная задача: Заданы приближенные значения A,B,C,D,…; F(A,B,C,D,…); d(F)≤ε Найти при каких значениях d(А), d(B), d(C), d(D) достигается заданная погрешность функции. Для решения обратной задачи нужны дополнительные условия на погрешности, иначе задача имеет много решений. Если же наложить условия оптимальности то задача сводится к условной либо безусловной оптимизации. Существует несколько вариантов упрощённых величин:

А) Вариант равных вкладов. Предполагается, что в первом приближении каждая величина даёт равный вклад: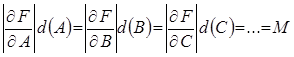

Пусть всего величин K. Значит 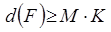и (M – первое приближение).

Б) Метод равных погрешностей.

В) Задача условной оптимизации.

Если использовать первое приближение и искать его минимум (min d₁(F)) при различных значениях погрешности, то получится задача линейного программирования; если будем использовать второе и более высокие приближения, то нужно использовать задачу нелинейного программирования. На практике используют вариант равных вкладов и равных погрешностей на задаче линейного программирования.

Дата добавления: 2015-07-11