
|
Читайте также: |
 , где
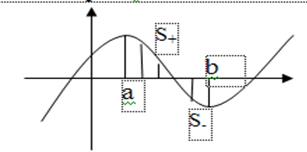
, где 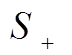 - площадь под кривой, там где функция >0.
- площадь под кривой, там где функция >0.  - площадь под кривой, там где функция <0.
- площадь под кривой, там где функция <0.
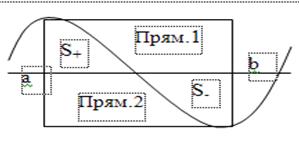
Рассмотрим прям.1 и проведем в нем эксперимент, найдем  . Проведем эксперимент в прям.2 и найдем
. Проведем эксперимент в прям.2 и найдем 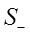 . Потом можно найти интеграл. Основания прям. одинаковые (от a до b), а высота разная (высота Прям.1
. Потом можно найти интеграл. Основания прям. одинаковые (от a до b), а высота разная (высота Прям.1  , а высота Прям.2
, а высота Прям.2  ). Если
). Если 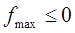 ,
, 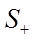 =0, значит, функция внизу; если
=0, значит, функция внизу; если  ,
, 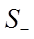 = 0, то функция вверху. Поэтому, чтобы найти интеграл одномерной функции, нужно найти максим. и миним. значения функции на этом отрезке, проверить
= 0, то функция вверху. Поэтому, чтобы найти интеграл одномерной функции, нужно найти максим. и миним. значения функции на этом отрезке, проверить 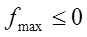 или
или  . Интеграл равен
. Интеграл равен 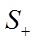 -
- 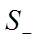 . Для того чтобы определить, что точка попадает в положительную область
. Для того чтобы определить, что точка попадает в положительную область  , при этом
, при этом  и
и  , при этом
, при этом 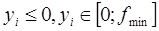 ,
,  .
.
Дата добавления: 2015-07-11; просмотров: 114 | Нарушение авторских прав