Вычисление координат точек замкнутого полигона.

Суммируют значение всех измеренных углов β полигона и практическую сумму . Вычисляют теоретическую сумму углов полигона , где n – число углов теодолитного хода. Определяют угловую невязку теодолитного хода . Вычисляют допустимую, или предельную угловую невязку . Сравнивают практическую невязку с допустимой 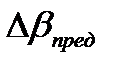, должна быть меньше . Распределяют невязку по целой минуте на те углы, которые расположены между короткими сторонами. Знак этих поправок должен быть обратным знаку невязки. Сумма исправленных углов должна равняться теоретической сумме. Вычисляют по исходному дирекционному углу дирекционные углы всех остальных линий хода ( и т.д.): и т.д. Дирекционный угол последующей линии равен дирекционному углу пре­дыдущей линии минус исправленный угол, лежащий справа по ходу между предыдущей и последующей линиями. Если дирекционный угол получился больше 360°, то необходимо из него вычесть 360°. Если после прибавления 180° к дирекционному углу исправлен­ный угол (3 не вычитается из пего, то необходимо добавить еще 360°, а затем вычесть исправленный угол β. Контролируют правильность вы­числения дирекционных углов, полу­чая исходный дирекционный угол че­рез дирекционный угол последней стороны и первый исправленный угол: . Переводят вычисленные дирекционные углы в румбы по формулам: (1 четверть, СВ), (2 четверть, ЮВ), ,(3 четверть, ЮЗ) (4 четверть, СЗ). Вычисляют приращения координат ∆x и ∆у по румбам (или дирекционным углам) и горизонтальным проложениям линий. Приращения координат ∆х и ∆у есть разность координат двух точек по оси Х и по оси У. Абсолютное значение приращения координат вычисляют по формулам и , где d-горизонтальное проложение, -дирекционный угол, r-румб. Перед значениями ∆x и ∆у ставят + или – согласно названию румба. Подсчитывают алгебраические суммы вычисленных приращений координат и .Для замкнутого полигона алгебраические суммы приращений координат теоретически должны равняться нулю, т.е. 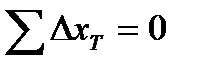, . Практические суммы вычисленных приращений не бывают равны нулю, а равны некоторым значениям. Которые называют линейными невязками в приращениях координат, т.е. , , где -линейная невязка по оси абсцисс, -то же, по оси ординат. Определяют абсолютную невязку в периметре теодолитного хода, которая представляет собой гипотенузу прямоугольного треугольника с катетами, равными и , т.е. . Допустимость абсолютной невязки определяется относительной невязкой, которая не должна превышать 1/2000 при измерении расстояний 20-метровой стальной лентой. Определяют относительную невязку в периметре теодолитного хода, для чего подсчитывают периметр теодолитного хода с округлением до сотен метров и вычисляют ее по формуле . Распределяют после подсчета относительной невязки и в виде поправок соответственно на все ∆x и ∆у с учетом следующих правил: значения поправок не должны быть прямо пропорциональны значениям горизонтальных проложений; знак поправок - обратный знаку невязки; абсолютная сумма всех поправок должна равняться невязке. Суммируют алгебраически каждую поправку с соответствующим приращением. Получают исправленные приращения. Суммируют исправленные приращения ∆x и ∆у, суммы которых должны быть равны нулю. По исходным координатам точки 1 и по исправленным приращениям ∆x и ∆у вычисляют координаты всех остальных точек теодолитного хода по формулам , , т.е. координата последующей точки равна координате предыдущей точки плюс соответствующее исправленное приращение. Так, , , , и т.д. Контроль – получение заданных координат точки 1: , .

38. Построение продольного профиля трассы.

После вычисления отметок всех пронивелированных точек приступают к построению продольного профиля и поперечников. Профиль строят на миллиметровой бумаге, на которой все размеры откладывают без измерителя. Для построения профиля надо в принятом масштабе для горизонтальных линий отложить все горизонтальные расстояния между пронивелированными точками, а в вертикальном направлении – все отметки этих точек в масштабе для вертикальных линий. Масштабы для горизонтальных линий принимают в 10 раз крупнее масштаба горизонтальных линий для наглядности (1:100,1:200,1:500,1:1000).Построение профиля начинают с вычерчивания профильной сетки, состоящей из нескольких горизонтальных линий и имеющей различные графы. Верхнюю линию профильной сетки, т.е. лини. Отметок земли, совмещают с одной из утолщенных линий на миллиметровой бумаге, а нижняя линия сетки должна быть на 4…5 см выше нижнего края листа. Заполнение графы «расстояние»: В этой графе откладывают в принятом масштабе для горизонтальных линий расстояния между пикетными точками. В промежутках между ними наносят в том же масштабе плюсовые точки и подписывают расстояния между ними и соседними пикетными точками. Иксовые точки на профиль не наносят. Затем под этой графой выписывают номера пикетов. Заполнение графы «отметки земли»: В эту графу записывают из журнала вычисленные отметки пикетных и плюсовых точек с округлением до сотых долей метра. Отметки всех точек откладывают от линии условного горизонта на вертикалях, проведенных через эти точки, в выбранном масштабе вертикальных линий. Соединив по рейке эти точки получают профиль трассы. Заполнение графы «план трассы»:План местности наносят по пикетажной книжке в принятом дл яданного профиля масштабе для горизонтальных линий в соответствующей графе профильной сетки.

Дата добавления: 2015-07-10