Читайте также:
|
По определению 
.
В координатном представлении
Введем безразмерный оператор 
такой, что
.
Используем 
Таким образом для оператора
.
.
.
.
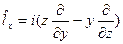Переход из декартовых координат в сферические координаты:
Переход из сферических в декартовы координаты
Также используем:
(29.1)
Переход при 
имеет вид
.
Тогда в общем виде
.
Из (29.1) имеем
.
Теперь найдем:
Таким образом
Аналогично имеем
§ 30. Коммутационные соотношения с оператором 
Раньше было получено:
и также
,
где 
- скалярный оператор.
Рассмотрим оператор 
.
Найдем коммутатор
или
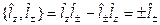
из этого имеем
Найдем произведение
Аналогично
Теперь для 
§ 31. Собственные функции и собственные значения операторов и 
Для соотношения были получены ранее:
Т. к. операторы и - коммутируют
они обладают общим базисом.
Было показано, что
,
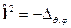тогда его собственная функция удовлетворяет уравнению
Произведем разделение переменных
В этом случае, запишем
Здесь 
можно рассматривать как множитель, т. к. оператор на нее не действует.
Ранее было показано
Усредним
Здесь мы имеем равенство только тогда, когда m=0 и 
.
Таким образом получаем ограничение на среднее
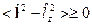
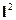и 
одновременно измеримы, т. к. они коммутируют. Это значит, что они одновременно измеримы и обладают общим базисом собственных функций. Тогда
.
Отсюда
,
Рассмотрим теперь соотношение
Подействуем этим оператором на функцию
для максимального 
, т. е.
.
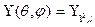Тогда
Так как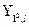 
- есть собственная функция оператора , то имеем
.
Обозначив
имеем
Это задача на собственные функции и собственные значения для оператора . Максимальное собственное значение для есть 
, но у нас 
. Таким образом 
.
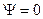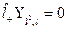
Подействуем оператором 
Тогда
Теперь
- орбитальное число.
Теперь
.
Выясняется, что
.
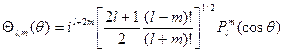Здесь 
- полином Лежандра.
Условие нормировки для записанных шаровых функций
Рассмотрим величину орбитального момента:
Тогда
При переходе к классической механике: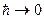 
. Определим величину предела 
.
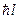В классической механике существует величина момента импульса, тогда при 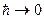мы не должны получать 0. Учтем произвол . Таким образом возникает 
. При этом
§ 32. Собственный механический момент (спин)
Рассмотрим Na. У него есть желтая линия. Возникает при переходе с уровня 3p на 3s.
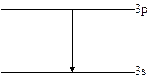
Первоначально ее длина была 5892 
Было обнаружено, что эта линия расщепляется на две: дублет.
Возникла идея расщепления уровня 3p на два, тогда можно объяснить возникновение двух линий.
Их длины: 5896 и 5890 .
В 1925 г. Была предложена гипотеза спина, т. е. собственного механического момента.
У электрона спиновое число s= 
.
Впоследствии Паули ввел спин в теорию.
Если имеем одну частицу, то она характеризуется орбитальным квантовым числом 
.
Составная частица (атом) состоит из многих микрочастиц. Можно рассматривать эту составную частицу в целом и приписать ей момент , который описывает орбитальное движение частицы как целого.
Энергетический уровень этой составной частицы в некоторых полях будет зависеть от орбитальных моментов микрочастиц 
.
Эти моменты являются внутренним свойством этой составной частицы.
Можно рассматривать 2 момента:
1) 
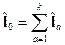. Этот момент описывает внутреннее движение частицы (относительно центра инерции)
2) Частица сама движется по некоторой траектории.
У частицы есть еще квантовое число 
, характеризующее собственный механический момент.
Вводят оператор собственного механического момента:
По аналогии
Спин – внутреннее свойство частицы. Его смысл – у частицы есть внутренний параметр, который реагирует на вращение координат независимо от места положения частицы.
Дата добавления: 2015-07-11; просмотров: 151 | Нарушение авторских прав