Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы

В случае бесконечно глубокой ямы по определению имеем

Интересующее нас решение ищем на отрезке

.

Поскольку в точках x=0 и x=a потенциальная энергия частица обращается в бесконечность, вероятность преодоления бесконечного барьера и попадания за пределы области равна нулю. Оказавшись в этой области частица все время будет находиться в ней. Из определения волновой функции следует

где в.ф. удовлетворяет стационарному уравнению Шредингера

совпадающему с определением оператора , т.е. функция есть собственная функция этого оператора, соответствующая собственному значению Е. Из сказанного вытекают граничные условия , накладываемые на решение уравнения.

Таким образом, приходим к задаче

От сюда следует:

(*)

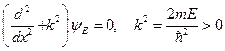Положительность собственного значения Е оператора вытекает из положительности . Решение уравнения (*) представимо в виде суперпозиции двух элементарных состояний, которые на языке интерпретируются как волны де Бройля, распространяющиеся в противоположных направлениях оси x:

Подстановка решения в граничные условия приводит к системе однородных уравнений

(**)

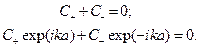Для неизвестных коэффициентов С_{+/_.} Критерий существования нетривиального решения данной системы

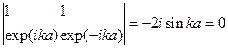
дает условие квантования

собственного значения Е. Это означает, что обладает дискретным спектром. Вводя согласно (**) обозначения

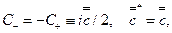
где С - неизвестная пока вещественная (в силу наличия у в.ф. произвольного фазового множителя) константа, для искомой в.ф. будем иметь

Поскольку собственные функции оператора с дискретным спектром квадратично интегрируемы, условие нормировки имеет вид

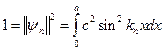
От сюда, интегрируя, получаем

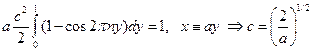
Подставляя найденное значение константы, запишем решение задачи в окончательной форме 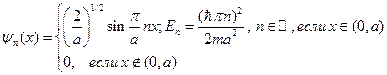(13.2)

Дата добавления: 2015-07-11