Мы писали волновое уравнение в виде

,

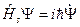здесь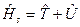

Для одной материальной точки :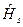

1. Без магнитного поля .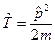

2. Если есть магнитное поле, то .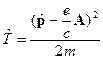

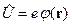
В этих случаях спин не учтен.

С учетом спина модификацию уравнений сделал Паули.

Примечание: уравнения Шредингера и Паули нерелятивистские.

Запишем уравнение Паули:

.

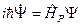
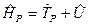Здесь изменился оператор кинетической энергии.

Без учета магнитного поля

,

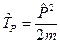где

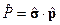
Здесь

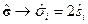- матрицы Паули

Тогда

.

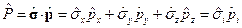Покажем, что при отсутствии поля, имеем

,

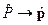т. е.

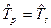
Рассмотрим

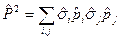={так как 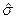действует на спиновую переменную, а на пространственную, то 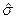и коммутативны.} = =

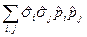={рассмотрим сумму когда 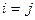и когда 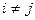}= =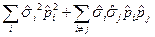{рассмотрим .

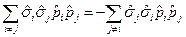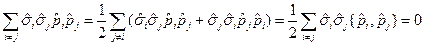, т. к.

}=[

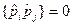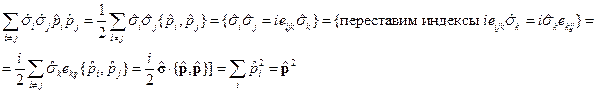
При :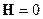

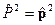
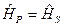
Рассмотрим случай когда есть магнитное поле:

.

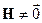Тогда для оператора 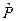имеем

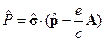
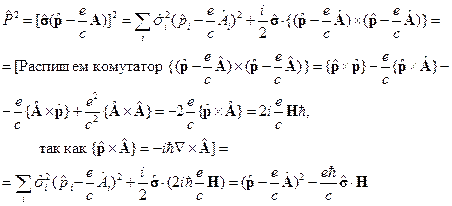
Тогда оператор кинетической энергии из оператора Паули:

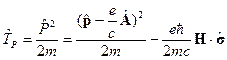
Рассмотрим случай электрона e<0.

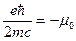(магнетон Бора)

Тогда в итоге получаем:

,

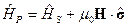где оператор

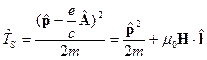
Для оператора Паули тогда получим

,

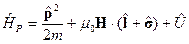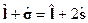
Отсюда видно равенство для гиромагнитных отношений

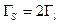
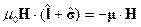
Видно, что магнитные моменты

,

,

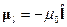механические моменты

Гиромагнитные отношения

.

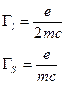Полный магнитный момент

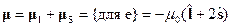
Дата добавления: 2015-07-11