Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближение

При n=2 возможно:

p=2, q=0; p=1, q=1; p=0, q=2.

Для членов второго порядка малости запишем из (3)

(9*)

Теперь запишем для второго порядка выражение (5*):

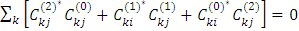(10*)

Рассмотрим случай i=j:

=

Получили поправку второго порядка малости к энергетическому уровню основного состояния. Пусть j- основное состояние (так как спектр невырожденный). Тогда знаменатель в поправке второго порядка всегда отрицательный. Тогда поправка всегда отрицательна.

Рассмотрим теперь (10*): его можно в общем случае записать, учитывая, что :

Рассмотрим случай i=j:

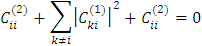
Из этого уравнения находим действительную часть , а мнимая часть обращается принудительно в ноль.

(11*)

Случай i≠j

Обычно пишут

Тогда

Дата добавления: 2015-07-11