Читайте также:
|
Рассмотрим оператор 
, который обладает дискретным спектром:
Под номером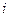 
понимается набор всех квантовых чисел, определяющих состояние системы.
– значения образующие энергетический спектр.
Так как спектр невырожденный, то между состоянием и уровнем (энергией) существует взаимооднозначное соответствие, т.е.:
Т.к. спектр дискретный, то функции квадратичноинтегрируемы:
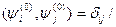
Пусть ЗШЛ решена и найдем собственные функции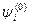 
и собственные значения 
.
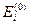Рассмотрим ЗШЛ:
.
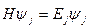
Оператор 
здесь имеет такую структуру, что эта ЗШЛ просто не решается, как ЗШЛ для операторы .
Оператор должен:
1. Иметь структуру 
, где – оператор для которого задача решена., 
– дает малую добавку в оператор.
2. Спектр собственных функций дискретен, тогда собственные функции квадратичноинтегрируемые
Решим задачу разложения по малому параметру (через теорию возмущений).
Из этого получаем
т.к. параметр малый, то энергетический спектр можно разложить по малому параметру:
p – указывает порядок разложения и показывает малость члена суммы.
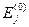отвечает невозмущенной задаче
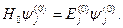
– поправка имеющая первый порядок малости.
Т.к. собственные функции оператора образуют базис, то по ним можно разложить собственные функции возмущенного оператора
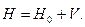
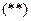
Коэффициенты разложения:
Их можно разложить по малому параметру:
Теперь задача теории возмущений состоит в нахождении членов рядов:
Чем больше членов рядов найдем, тем точнее решим задачу.
Подставим 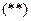в и вынесем коэффициенты за знак операторов
Используем решение для невозмущенного операторы
Обозначим этот ряд 
, где 
, тогда
Используем соотношение
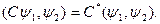
Коэффициенты выносятся за знак скалярного произведения:
Рассчитаем
– это матричный элемент оператора возмущений, который рассчитывается по невозмущенным функциям.
Тогда имеем
Получили матричное уравнение, которое должны разложить по малым параметрам и прировнять к 0 все слагаемые соответствующие своим порядкам малости.
считается величиной первого порядка малости, по нему проводится разложение.
Используем, что
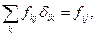
Здесь
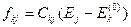
Тогда
Получили исходное уравнение. К чему еще добавляются две нормировки:
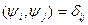
Подставим в уравнение выражения
Группируем члены по порядку малости. По каждому порядку должны получать справа ноль.
Сначала нулевой порядок
Так как имеет первый порядок малости то член связанный с ним будет отсутствовать.
Из этого выражения получаем что, так как спектр невырожденный, при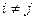 
Дает 
и получаем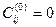 
, а при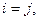 
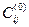может быть 
Легко видеть, что так как
,
то нулевое приближение дает
.
Тогда в нулевом приближении имеем решение:
Теперь для уровней:
.
Окончательно в результате нулевого приближения
Перейдем к первому приближению.
Получим дополнительные соотношения из условия нормировки возмущенных
функций.
Так как
получим
.
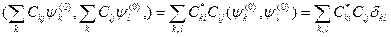Подставим сюда разложение по малому параметру
,
тогда имеем
Здесь справа стоит величина нулевого порядка малости.
для 
, 
.
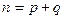для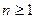 
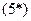
Рассмотрим первое приближение: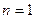 
. Два случая 
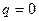и 
, 
и 
.
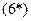
Из 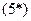имеем
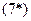
Используем, что
Тогда из 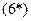и :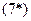
. 
Из рассмотрим случай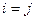 
:
- поправка к i-ому энергетическому уровню первого порядка малости.
Тогда в первом приближении
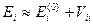
и также получаем
.
Тогда получили, что
,
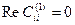т.е. коэффициенты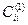 
чисто мнимые.
Ввиду неопределенности фазового множителя при волновой функции, то полагают
,
тогда принимают 
.
Из рассмотрим случай .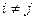
.
Подставим это выражение в и проверим условие нормировки:
.
Распишем
Получили истинность условия нормировки.
Тогда в первом приближении теории возмущений получили:
.
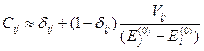Нам необходимо найти волновые функции, для них
Дата добавления: 2015-07-11; просмотров: 79 | Нарушение авторских прав