Читайте также:
|
Введем обозначение 
оператор, который осуществляет перестановку a-ой и b-ой частицы из ансамбля одинаковых частиц.
Оператор 
для таких систем из одинаковых частиц обладает симметрией.
Так как частицы одинаковые, то они имеют одинаковую энергию взаимодействия, т. е. она инвариантна относительно перестановки.
Т. е. можно записать
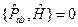(44.1)
Так как оператор явным образом от времени не зависит, то из (44.1) следует, что он является интегралом движения. Его собственные значения сохраняются.
Найдем собственные значения оператора .
Запишем задачу на собственные функции и собственные значения:
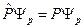(44.2)
При повторном действии оператора , получим:
(44.3)
С учетом (44.2):
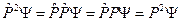
Тогда из (44.3)
, 
.
Получаем частицы с симметричными и антисимметричными волновыми функциями: бозоны и фермионы.
Кроме того, оператор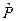 
- это интеграл движения. Тогда его собственные значения сохраняются во времени. Т. е. свойства волновых функций, связанных с действием этого оператора тоже сохраняются.
Функции отвечающие собственному значению +1 называются симметричными, описывают симметричные состояния.
Аналогично
Это антисимметричная функция.
Свойства симметричности и антисимметричности называются интегралами движения, т. е. сохраняются. Ансамбль не может переходить из одного состояния в другое (т. е. из симметричного в антисимметричное и наоборот).
Симметричные функции описывают состояние систем с целым спином, т. е. ансамбль бозонов.
Антисимметричные функции – ансамбль фермионов.
Пусть
,
где
,
, 
.
Мы будем рассматривать стационарные состояния, т. е.
,
где
.
Стационарные функции удовлетворяют стационарному уравнению Шредингера
,
так как операторы 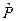и коммутируют, то
.
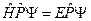Мы имеем
Если всего N частиц, то можно осуществить N! перестановок, тогда имеем N! возможных функций 
.
Так как все удовлетворяют уравнению Шредингера при одной и той же энергии 
, то мы получили вырождение. Оно носит фиктивный характер. Для того чтобы избавиться от этого вырождения проведем симметризацию функций.
Дата добавления: 2015-07-11; просмотров: 135 | Нарушение авторских прав