Читайте также:
|
Все проводится по аналогии с 
и 
.
обладает коммутационными свойствами:
Так как и 
не коммутируют, то они одновременно не измеримы.
Но 
.
Собственные значения оператора:
, 
.
Тогда здесь всего 2s+1 значение оператора.
Перейдем к классическому пределу: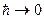 
Ввиду связи 
имеем 
, 
.
Ясно, что так как 
- параметр частицы, то он не меняется ни при каких условиях, тогда в классическом пределе:
, 
.
В классической механике этим величинам аналога нет и они обращаются в нуль.
В случае спина мы не можем наложить условие 
, т. к. спин – внутреннее свойство частицы. Тогда 
не всегда целое число.
Если 
- четное, то -полуцелое.
Если - нечетное, то -целое.
Отсюда деление на 2 типа частиц:
1) Фермионы – спин полуцелый
2) Бозоны – спин целый.
Дата добавления: 2015-07-11; просмотров: 54 | Нарушение авторских прав