Стационарное состояние различных систем

Задача на собственные функции и собственные значения для оператора :

(25.1)

Волновое уравнение:

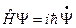(25.2)

Как только поставили в соответствие системе оператор , то можем решать волновое уравнение, находим , которая определяет состояние системы.

Собственные функции задачи (25.1) и функции, являющиеся решением волнового уравнения совпадают при условии выполнения:

, тогда . Это условие совместности решений (25.1) и (25.2).

Так как , то гамильтониан системы явно от времени не зависит, т. е. поле стационарно (задача стационарна) – это говорит о совместности решений (25.1) и (25.2).

Рассмотрим стационарную задачу , тогда не зависит от времени. Это либо:

Замкнутая система.

Система в стационарном внешнем поле.

Используя (25.1) и (25.2), получим

Это дифференциальное уравнение имеет решение

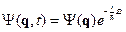
Подставим эту функцию в (25.1), тогда

.

Тогда получим

Получили стационарное уравнение Шредингера.

Дата добавления: 2015-07-11