
Читайте также:
|
Канонически сопряженные величины одновременно неизмеримы – это принцип неопределенности.
Под канонически сопряженными понимаем величины  и
и 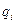 .
.
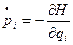

В квантовой механике для операторов 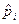 и
и  , которые поставлены в соответствие канонически сопряженным величинам имеем
, которые поставлены в соответствие канонически сопряженным величинам имеем
 .
.
Более того  , а сам коммутатор
, а сам коммутатор 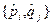 имеет вид оператора
имеет вид оператора  .
.
Это можно записать в виде  .
.
Если  , то
, то  , тогда
, тогда  , где
, где 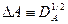 .
.

 , т.к.
, т.к.  и
и  есть числа.
есть числа.
Обозначим  . Здесь
. Здесь  - единичный оператор.
- единичный оператор.
Тогда из  получим
получим  (*)
(*)
Введем обозначение
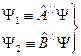
Подставим это в неравенство Коши-Шварца, тогда

Используем эрмитовость операторов
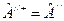 ,
,
 ,
,
тогда
 .
.
Поделим левую и правую части на  , тогда
, тогда

Используем определение среднего
 ,
,
тогда
 .
.
Или
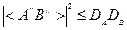
Операторы  и
и  не коммутируют, тогда
не коммутируют, тогда
 .
.
Первое слагаемое обозначим  ,
,  .
.
Второе слагаемое 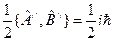 .
.
Оператор  дает чисто вещественное число, а
дает чисто вещественное число, а  дает чисто мнимое число.
дает чисто мнимое число.
Тогда
 ,
,
где  .
.
 .
.
Окончательно
 .
.
В полученном неравенстве математически заложен принцип неопределенности Гайзенберга.
Если величина измерена точно, то 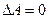 ,т.е.
,т.е.  .
.
Если 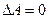 , то величина A измерена точно и
, то величина A измерена точно и  , но тогда для
, но тогда для 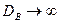 , т. к.
, т. к.  . Из этого следует, что канонически сопряженная величина B не измерима.
. Из этого следует, что канонически сопряженная величина B не измерима.
Когда измеряем величину 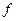 , то получаем спектр значений
, то получаем спектр значений  , которые выходят с вероятностью
, которые выходят с вероятностью  . Для того чтобы
. Для того чтобы  необходимо чтобы система находилась в состоянии
необходимо чтобы система находилась в состоянии  .
.
Дата добавления: 2015-07-11; просмотров: 107 | Нарушение авторских прав