Флуктуации физических величин

Пусть есть 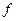- физическая величина, которая при измерении с вероятностью W_i дает величину , тогда мы можем говорить о среднем и о дисперсии 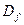, где

.

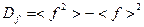Мы вводили флуктуацию

,

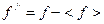отклонение величины 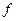от ее среднего значения.

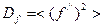
Перенесем все это на язык квантовой механики, т. к. физической величине 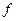мы ставим в соответствие .

Можно показать, что .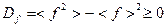

Неравенство Коши-Шварца: Оно справедливо и для функциональных пространств, в том числе и для Гильбертова пространства, которое рассматривается в квантовой механике.

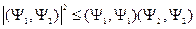
Для двух векторов оно имеет вид

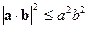
имеет смысл тот, что .

, .

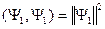Теперь, если обозначить 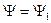, , 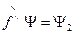тогда будем также рассматривать статистическое усреднение 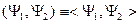. Отсюда получим из неравенства Коши-Шварца:

Теперь, если определить . К тому же по определению из 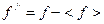имеем 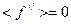, тогда 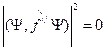. Из этого следует, что

.

В случае квантовой механики 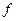заменяем на , тогда

.

Задача. Для стационарного состояния частицы в бесконечно глубокой потенциальной яме найти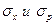

Дата добавления: 2015-07-11