Потенциальный барьер конечной высоты

Под потенциальным барьером понимают область пространства, где потенциальная энергия частицы увеличивается, а потом уменьшается. Как известно, в квантовой физике частица с некоторой вероятность может пройти сквозь потенциальный барьер.

Запишем уравнение Шредингера:

Для первой и третьей области уравнение запишется как

Для второй области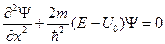

Решая уравнение Шредингера для каждой области, запишем волновые функции.

Где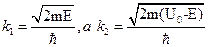

Введем нормировку на единичный поток, то есть положим C₁ =1.

«Сошьем» решения на границе областей, используя граничные условия (непрерывность в.ф. и ее производной на границе областей (конечный скачок U)):

Расписывая, получаем

Получили систему относительно переменных C₂, C₃, B₁, B₂. Решим её по правилу Крамера.

Теперь мы можем найти все неизвестные коэффициенты по формуле :

Отсюда мы можем найти коэффициенты прохождения и отражения. По определению . В нашем случае, коэффициенты будут равны

Дата добавления: 2015-07-11