Читайте также:
|
Этот вопрос идентичен вопросу рассмотренному в классической механике - будут те же соотношения, но для операторов
.
Поставим в соответствие конкретной системе операторы 
и 
:
В декартовой системе координат 
, 
.
Здесь n – число точек в системе.
.
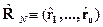- функция от оператора координаты.
Мы рассматриваем 
- представление, здесь
Мы рассматриваем декартову систему координат. Гамильтониан 
мы поставили в соответствие системе материальных точек. Эта система незамкнутая, т. к. потенциальная энергия зависит от времени. (т. е. здесь нет однородности времени).
Перейдем к более простой задаче. Рассмотрим систему N материальных точек во внешнем стационарном поле
Здесь 
отвечает за внутреннее взаимодействие между частицами.
отвечает за внешнее воздействие на систему частиц.
.
Выражение, описывающее внешнее воздействие обладает аддитивностью, т. е.
.
Индекс a означает, что разные частицы могут взаимодействовать с внешним полем по разному закону. Если все частицы одинаковые и одинаково взаимодействуют с внешним полем, то индекс a убирается.
Внутреннее взаимодействие 
неаддитивно.
Рассмотрим случай свободной материальной точки. Соответственно она ни с чем не взаимодействует:
Тогда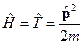 
, или в -представлении, то
,
тогда 
.
Если материальная точка во внешнем поле:
, 
,
Нестационарное поле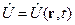 
.
Стационарное поле 
.
Центральное поле 
.
Рассмотрим систему двух материальных точек. Мы рассматриваем частный случай – замкнутая система двух материальных точек.
В случае классической механики: 
.
Отсутствие t в энергии взаимодействия – это однородность времени и закон сохранения энергии.
Зависимость энергии от модуля 
есть изотропность пространства.
В квантовой механике в -представлении:
,
,
где
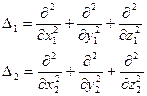
Дата добавления: 2015-07-11; просмотров: 86 | Нарушение авторских прав