Читайте также:
|
Надо сформулировать уравнение функции, которая описывала бы квантово-механическую систему.
Это уравнение было получено Шредингером интуитивным путем. Оно ниоткуда не выводится.
Приведем некоторые соотношения в пользу уравнения Шредингера:
Норма волновой функции: 
- вероятность обнаружить динамические переменные в интервале 
.
Наложим на 
- условие ее сохранения во времени. 
- это физическое требование, поскольку 
, то 
также функция времени.
На базе ограничения получим некоторые ограничения на 
.
Обозначим 
. Мы знаем, что 
, таким образом 
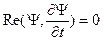. Тогда само скалярное произведение 
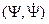- чисто мнимое число.
Но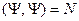 
- число вещественное. Отсюда можно представить
(19.1)
Здесь мнимая единица из соотношения 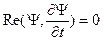. Т. к. в (*) стоит линейный оператор 
, то это соотношение удовлетворяет принципу суперпозиции.
Подставим (19.1) в равенство 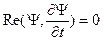, тогда
- эта величина должна быть чисто вещественной, тогда оператор - эрмитов: 
.
Свойства оператора :
В пределе перехода к классической механике: 
, то 
, где S – действие из классической механики. Причем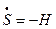 
, тогда рассматривая
, (19.2)
где 
- функция Гамильтона.
В нашем случае 
, тогда учитывая предельный переход и (19.2), то: 
.
Получили волновое уравнение:
- нестационарное уравнение Шредингера (волновое уравнение).
Каждой системе ставится в соответствие Гамильтониан, решаем с гамильтонианом уравнение Шредингера и получаем волновую функцию которая определяет эволюцию системы.
Дата добавления: 2015-07-11; просмотров: 156 | Нарушение авторских прав