Транспонированный оператор

Отметим следующие свойства:

1)

(10.1)

Из выражения (10.1) получаем:

2)

3)

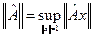
Сумма операторов: . Это операторное равенство предполагает

Произведение операторов: , тогда . Это операторное равенство предполагает

В общем случае не коммутативны

Коммутатор

Если , то операторы и называются коммутативными (операторы и коммутируют).

Если , то операторы и называются не коммутативными (операторы и не коммутируют).

Так как физические величины вещественны, то число операторов в квантовой механике ограничено. Собственные значения эрмитовых операторов вещественны, значит только их можно ставить в соответствие физическим величинам.

Запишем определение среднего:

Так как результаты измерений вещественны, то тоже должно быть вещественным, т.е.

(10.2)

тогда

,

т.е.

Обозначим , тогда

Тогда из (10.2) получаем

(10.3)

Из (10.3) имеем для любых :

,

,

где 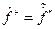(сопряженный и транспонированный).

Дата добавления: 2015-07-11