Читайте также:
|
Имея в распоряжении несколько простых операторов можно получить из них более сложные.
Суммой операторов 
и 
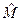называют оператор 
, который определяется следующим образом:
.
Символически это записывается так:
.
Например, 
Произведением операторов и 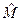будем называть оператор , который определяется следующим образом:
,
причем на функцию сначала действуем ближайшим к ней оператором, а потом на полученный результат – следующим,
.
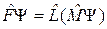Символически произведение операторов записывается в виде 
.
Например, 
. Подействуем произведением этих операторов на функцию 
:
.
Если действие одного и того же оператора повторяется n раз, это записывается в виде степени этого оператора:
.
Например,
.
Произведение операторов зависит от порядка множителей. Например, если 
, то 
Но 
. Очевидно, что в этом случае 
. Таким образом, операторы, вообще говоря, являются некоммутативными (неперестоновочными). Если 
, то операторы называют комутирующими. В этом случае 
. Выражение 
называют коммутатором.
Дата добавления: 2015-07-11; просмотров: 236 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Операторы динамических переменных. | | | Собственные функции и собственные значения оператора. |