Читайте также:
|
Вид оператора данной физической величины зависит от выбора независимых переменных в функциях, к которым он применяется.
а) Оператор независимой переменной всегда представляет собой операцию умножения на эту переменную. Это вытекает из постулата (в нашем пособии - третьего), согласно которому полученные при измерении значения физической величины совпадают с собственными значениями ее оператора. Например, если в системе с одной степенью свободы независимой переменной является координата 
, т.е. 
, то оператором координаты будет операция умножения на : 
.
При наличии нескольких степеней свободы следует выяснить, любое ли сочетание физических величин может являться набором независимых переменных. Операторы независимых переменных являются умножением на эти переменные. Поэтому они должны коммутировать (быть коммутативными). Следовательно, в качестве независимых переменных можно брать только такие величины, операторы которых между собой коммутируют.
б) Найдем оператор импульса при условии, что координата является независимой переменной. Как известно, (согласно идеям де Бройля, подтвержденным экспериментально), волновая функция свободной частицы есть монохроматическая волна
.
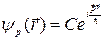(Момент времени фиксирован).
Для одномерного случая, когда частица движется вдоль оси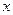 
,
.
Поскольку частица свободна, т.е. нет никакого взаимодействия, ее импульс сохраняется и равен 
. Таким образом, собственная функция оператора 
есть 
и ей соответствует собственное значение 
. Поэтому можно записать уравнение собственных значений:
.
Это соотношение будет справедливым если 
. Действительно, 
. Рассуждая аналогично, получаем 
, 
и 
.
Дата добавления: 2015-07-11; просмотров: 86 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дельта-функция Дирака. | | | Соотношение неопределенностей. |