Понятие гильбертова пространства.

Из принципа суперпозиции следует, что уравнения квантовой механики должны быть линейными. Действительно, если 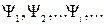являются решением такого уравнения, то также должно быть его решением.

Из принципа суперпозиции следует также, что состояния системы в квантовой механике должны описываться такими математическими величинами, которые можно складывать, умножать на комплексные числа и при этом получать величины такого же типа.

Таким образом, величины, характеризующие состояние квантовомеханической системы, можно считать элементами некоторого линейного функционального пространства. Что же это за пространство? Ранее мы показали, что -функции являются, как правило, квадратично-интегрируемыми, т.е. такими, что

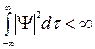
(Здесь 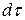– произведение дифференциалов независимых переменных от которых зависит -функция. Интегрирование проводится по всей области изменения этих переменных). Следовательно, каждой -функции можно сопоставить число

(1.3.1)

Это число называется нормой функции .

Существует аналогия между и абсолютной величиной вещественного или комплексного числа. С помощью абсолютной величины производится измерение расстояний на числовой оси

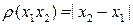
Аналогично понятие нормы даёт возможность множество элементов (функций) рассматривать как некоторые «пространство», в котором также можно проводить измерения. Расстояние между элементами и определяется числом

Таким образом, множество функций, характеризующих состояние квантовомеханической системы, образуют метрическое пространство. Оно называется пространством Гильберта. В этом пространстве можно определить скалярное произведение функций:

. (1.3.2)

Если скалярное произведение равно нулю:

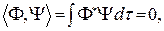
то функции и считают ортогональными. Норма определяется через скалярное произведение функции саму на себя:

.

Свойства скалярного произведения:

(1.3.3а)

(1.3.3б)

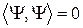, только если (1.3.3в)

Из соотношения (1.3.3а) следует, что скалярное произведение комплексной функции саму на себя вещественно:

Указанные свойства -функции аналогичны свойствам векторов в евклидовом пространстве. Эту аналогию рассмотрим подробнее при изучении операторов квантовой механики.

Итак, множество состояний квантовомеханической системы может быть представлено как пространство Гильберта.

Гильбертово пространство есть множество элементов (в нашем случае – функций, характеризующих состояние квантовой системы), на котором определены операции сложения, умножения на число и скалярное произведение с указанными выше свойствами (1.3.3).

Вопросы для самопроверки.

1. Сформулировать первый постулат квантовой механики.

2. Какая связь между -функцией системы и вероятностью результатов измерения физических величин в данном состоянии?

3. Сформулировать принцип суперпозиции состояний.

4. Объяснить, чем квантовомеханическая суперпозиция отличается от классической?

5. Охарактеризуйте понятие "пространство Гильберта".

Дата добавления: 2015-07-11