
Читайте также:
|
1.1. Частица локализована в области 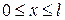 на оси
на оси  и ее состояние описывается функцией
и ее состояние описывается функцией  . Найти коэффициент нормировки.
. Найти коэффициент нормировки.
1.2. Состояние частицы, локализованной на оси  в интервале
в интервале  описывается функцией
описывается функцией  . Найти вероятность ее обнаружения в области
. Найти вероятность ее обнаружения в области 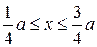 .
.
1.3. Состояние частицы в данный момент времени  описывается волновой функцией
описывается волновой функцией  , представляющей собой суперпозицию волн де Бройля с одинаковыми амплитудами
, представляющей собой суперпозицию волн де Бройля с одинаковыми амплитудами 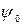 и мало отличающимися волновыми числами в интервале
и мало отличающимися волновыми числами в интервале  . Определить распределение плотности вероятности местонахождения частицы и размер области ее локализации.
. Определить распределение плотности вероятности местонахождения частицы и размер области ее локализации.
1.4. В момент времени 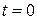 волновая функция частицы имеет вид
волновая функция частицы имеет вид  , где
, где 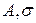 и
и  – постоянные. Определить нормировочный коэффициент
– постоянные. Определить нормировочный коэффициент  , изобразить примерный вид зависимости
, изобразить примерный вид зависимости  от
от  и область локализации частицы.
и область локализации частицы.
Указание. Распределение вероятностей, описываемое плотностью вида

называется нормальным или гауссовским,  – среднее значение случайной величины,
– среднее значение случайной величины,  – ее дисперсия.
– ее дисперсия.
1.5. Частица локализована на оси  в области
в области  и ее состояние описывается функцией
и ее состояние описывается функцией

Вычислить среднее значение ее координаты  и дисперсию
и дисперсию  .
.
Дата добавления: 2015-07-11; просмотров: 135 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Понятие гильбертова пространства. | | | Операторы динамических переменных. |