Читайте также:
|
Волновая функция динамических переменных и времени определяет состояние системы с точностью до фазового множителя, т. е.
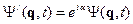
т. е. 
и 
описывает одно и тоже состояние, где 
- фазовый множитель. Волновая функция – комплексная, непрерывная, конечная. У нее почти всюду существует конечная производная по координате, но в некоторых точках может терпеть скачек (особые точки). Функции - нормируемые, т.е. квадратично интегрируемы. Но для свободной материальной точки не нормируема.
- элементарный объем
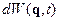- вероятность того, что динамические переменные 
лежат в интервале 
. Это определение справедливо для квадратично интегрируемых функций. Для не квадратично интегрируемых функций величина 
пропорциональна плотности вероятности.
Дата добавления: 2015-07-11; просмотров: 94 | Нарушение авторских прав