Матрицы Паули и их свойства

Рассмотрим электрон со спином 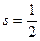. Тогда матрицы, которые будут представлять спиновые моменты имеют размерность

.

Рассмотрим представление (или 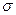- представление). Рассмотрим в этом представлении матрицу Это оператор в матричном представлении.

Мы помним, что в матричном представлении ядро оператора имело вид

.

Тогда для нашего представления имеем:

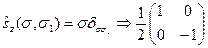
Аналогично матрицы

,

,

.

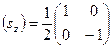и 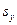не диагональные матрицы, тогда эти величины с одновременно не измеримы. По главной диагонали стоят собственные значения.

Вводятся матрицы . Это матрицы Паули.

Тогда

,

,

.

Легко показать, что

.

Или на языке операторов

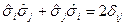
А коммутаторы:

,

.

Тогда так как 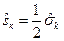, то получим

При :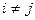

Тогда

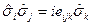
При 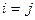получаем

.

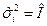Дата добавления: 2015-07-11