
|
Читайте также: |
Рассмотрим одну частицу – система с 3 степенями свободы. Задача решается в  - представлении.
- представлении.
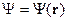 ,
,
но есть еще внутренний параметр – спин, тогда
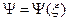 .
.
Здесь  - переменная
- переменная  (пространственная координата) и
(пространственная координата) и 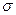 (спиновая переменная, а именно проекция спина на ось
(спиновая переменная, а именно проекция спина на ось  ).
).
Здесь мы рассматриваем стационарную задачу, поэтому  от t не зависит.
от t не зависит.
Скалярное произведение теперь запишем в виде

Вероятность обнаружения частицы 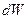 в объеме
в объеме  вблизи точки
вблизи точки  :
:
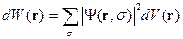
Если хотим найти реализацию конкретного значения 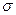 :
:
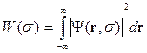
Рассмотрим действие операторов в пространстве четырех переменных
Было известно
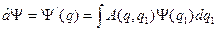 (40.1)
(40.1)
Обобщим (40.1) на случай четырех переменных:
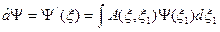 (40.2)
(40.2)
Рассмотрим случай когда 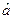 действует только на спиновую переменную. В этом случае ядро будет следующим
действует только на спиновую переменную. В этом случае ядро будет следующим
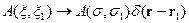
и интеграл (40.2) переходит в интеграл:
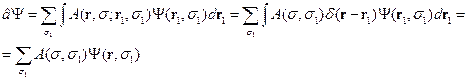
Тогда

Переменная  здесь не играет большой роли. В дальнейшем будем ее опускать, тогда
здесь не играет большой роли. В дальнейшем будем ее опускать, тогда
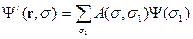
Функция 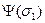 имеет 2s+1 переменную.
имеет 2s+1 переменную.
Ядро 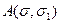 в дискретных переменных вырождается в матрицу, т. е. это есть матрица размером
в дискретных переменных вырождается в матрицу, т. е. это есть матрица размером 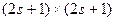 .
.
Дата добавления: 2015-07-11; просмотров: 63 | Нарушение авторских прав