Симметричное и антисимметричное состояния

Чтобы построить конкретные функции будем рассматривать ансамбль независимых частиц, т. е. они между собой не взаимодействуют, но могут находиться во внешнем поле.

Для i -ой частицы во внешнем поле:

Так как частицы одинаковые, то их массы одинаковые, т. е. .

Полный оператор

(45.1)

Для 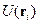одинаковые аналитические выражения (закон один), но здесь разные координаты.

Когда оператор представим в виде (45.1), то можно провести разделение переменных

.

Тогда уравнение

разбивается на N одинаковых уравнений:

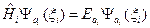
- волновая одночастичная функция.

- это набор квантовых чисел, характеризующих одночастичное состояние.

Тогда

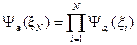(45.2)

- это все квантовые числа, относящиеся к рассматриваемому ансамблю.

Причем

,

где

.

Учтем действие оператора перестановки:

1) Рассмотрим симметричные состояния.

Однако из (45.2) при перестановке мы получаем другую функцию. Но в (45.2) функция еще не симметричная. Симметризуем ее:

Здесь сумма по всем нетождественным перестановкам частиц.

- постоянная нормировки

,

где

.

Рассмотрим случай двух частиц

Для данного случая

.

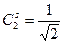Так как бозоны могут находиться в неограниченном количестве в одном и том же состоянии, то здесь когда говорим о нетождественных состояниях, то имеем в виду, что эта перестановка приводит к новому состоянию.

Если перестановка происходит в одном и том же состоянии, то она тождественная и выбрасывается из рассмотрения. Для бозонов из N! перестановок 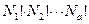тождественные перестановки. Тогда надо рассматривать 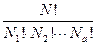перестановок, где N всего бозонов, а в 1-ом состоянии находится N₁ частиц, во 2-ом N₂ частиц и тд.

Симметричные состояния допускают произвольное число частиц в одночастичном состоянии.

Тогда нормировочный множитель

2. Рассмотрим антисимметричные состояния

Здесь

(45.3)

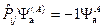
Чтобы учесть знак вводят понятие парной (соседней, элементарной) перестановки.

Пусть надо переставить в ряде 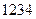цифры 1 и 4. Учтем элементарные перестановки:
2134, 2314, и т. д.

Здесь 5 элементарных перестановок. .

Тогда в сумму (45.3) надо поставить .

Если i и j в одном состоянии, то , => .

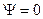Антисимметричные состояния запрещают нахождение более одной частицы в одночастичном состоянии.

В сумме (45.3) оператор 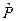это оператор не элементарной перестановки, а какой-то конкретной перестановки.

Итак получаем из (45.3) выражение

Рассмотрим пару частиц, тогда

Эта функция обладает свойством антисимметричности. Подействуем на нее оператором перестановки:

,

т. е.

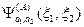- собственная функция оператора перестановки.

Здесь 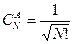т. к. у фермионов в каждом одночастичном состоянии число частиц не превышает 1, т. е. 0 или 1.

В наиболее общем виде

.

Обобщим

Из этого вида вытекает принцип Паули: не более одного фермиона может находиться в одном квантовом состоянии.

Допустим две частицы в одном квантовом состоянии, тогда у них совпадают квантовые числа, т. е. . Тогда для детерминанта имеем 2 одинаковые строки, он равен нулю. Состояние не реализуется.

Дата добавления: 2015-07-11