Стационарная теория возмущений в случае близких энергетических уровней.

Пусть у нас два близких уровня, а остальные уровни хорошо удовлетворяют критерию (5).

Пусть близкие уровни - это уровни i=1,2. Близость уровней определяется из критерия (5).

Модификация теории возмущений состоит в том, чтобы в качестве нулевого приближения для 1 и 2 состояния подобрать такие функции и , которые обращали бы в ноль - числитель критерия (5).

По определению:

Мы рассмотрим набор

Очевидно, что

Распишем:

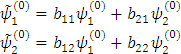
Рассмотрим свойства невозмущенной функции:

Они удовлетворяют ЗШЛ:

где - невозмущенный оператор.

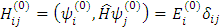(6)

Эта матрица имеет диагональный вид, т. к. мы рассматриваем матричные элементы на собственных функциях этого оператора.

Мы ввели и для того, чтобы ввести такой матричный элемент, чтобы он

тогда (5) будет для и давать 0 и теория возмущений будет работать.

Таким образом, мы ввели новый возмущенный базис и . В этом новом базисе мы должны диаганализовать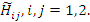

Искомое преобразование является унитарным, так как оно не нарушает условия нормировки. Надо подобрать коэффициенты

Используем

Но

или в матричном виде

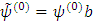
Из свойства ортонормированности найдем свойства коэффициентов

т.е.

Это унитарное преобразование, оно сохраняет нормировку.

Запишем ЗШЛ для модифицированных функций.

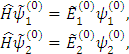
тогда подставим явно и

Рассмотрим случай i=1, умножим левую и правую части этого уравнения скалярно на и , тогда имеем:

Введем обозначения:

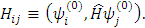
Перепишем эти уравнения в виде

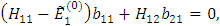(7)

Система линейных однородных уравнений. Она имеет нетривиальное решение только при det=0.

Обозначим

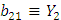
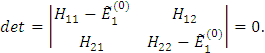
Имеем решение

При i=2, то по аналогии

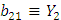
и обозначив

получаем

Во втором случае решение аналогично первому. Однако мы приписываем одному знак +, а другому -.

Имеем тогда уровни энергии:

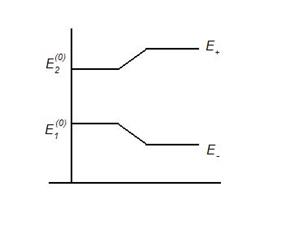
Перейдем к системе (7). Из нее имеем

Кроме этого используем соотношение

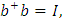
т.е. имеем нормировку

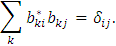
Рассмотрим i=j=1 (и аналогично i=j=2)

Введем обозначение:

где α и β – вспомогательные углы, определяемые через матричные элементы H ₁₂, H ₁₁ и H ₂₂.

Тогда коэффициенты b имеем в виде

Таким образом, при теория возмущений срабатывает для двух близких уровней. Теперь в качестве нулевого приближения берут:

Модификация касалась только этих дух близких состояний. Остальные состояния не модифицировались, т.к. они сразу удовлетворяли критерию.

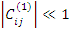Теперь и – теория возмущения работает.

Задачи по курсу «Квантовая статистика»

Дата добавления: 2015-07-11